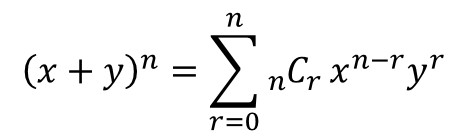Properties of Pascal’s Triangle
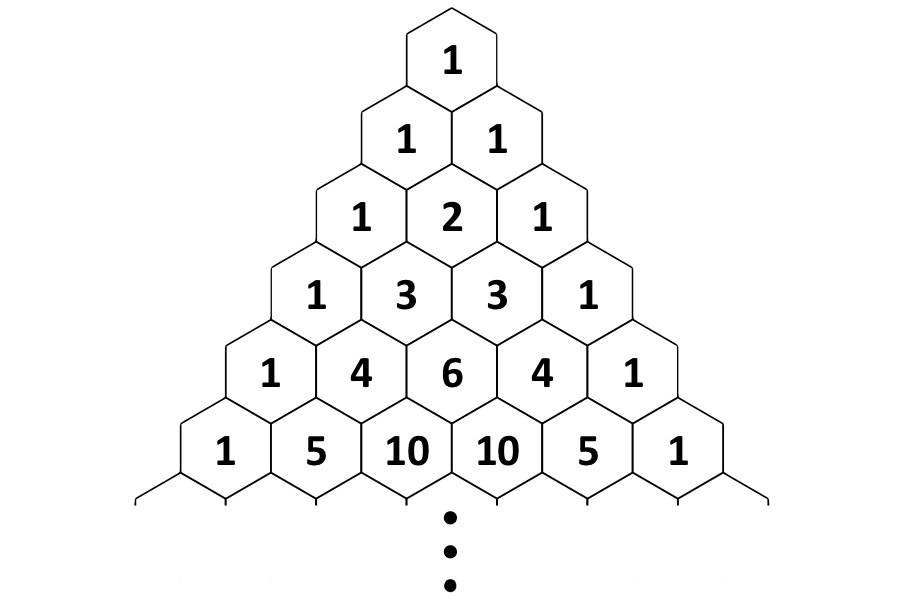
Pascal’s triangle is a never-ending equilateral triangle of numbers that follow a rule of adding the two numbers above to get the number below. Two of the sides are “all 1's” and because the triangle is infinite, there is no “bottom side.”
It is named for Blaise Pascal, a 17th-century French mathematician who used the triangle in his studies in probability theory. However, it has been studied throughout the world for thousands of years, particularly in ancient India and medieval China, and during the Golden Age of Islam and the Renaissance, which began in Italy before spreading across Europe.
Simple as this pattern is, it has surprising connections throughout many areas of mathematics, including algebra, number theory, probability, combinatorics (the mathematics of countable configurations) and fractals. In a 2013 "Expert Voices" column for Live Science, Michael Rose, a mathematician studying at the University of Newcastle, described many of the patterns hidden in Pascal's triangle. In this article, we'll delve specifically into the properties found in higher mathematics.
Combinations
Pascal’s triangle arises naturally through the study of combinatorics. For example, imagine selecting three colors from a five-color pack of markers. The order the colors are selected doesn’t matter for choosing which to use on a poster, but it does for choosing one color each for Alice, Bob, and Carol. The number of possible configurations is represented and calculated as follows:
- One color each for Alice, Bob, and Carol: A case like this where order does matter is called a permutation. For a case with five options where three will be chosen and ordered, this number of possible permutations is expressed as 5P3 and calculated as 5!/(5-3)!. The operator “!” is called a factorial, which means multiply all the lesser whole numbers down through one (e.g. 5! = 5 × 4 × 3 × 2 × 1) The expression for 5P3 simplifies to 5!/2! = 5 × 4 × 3 = 60
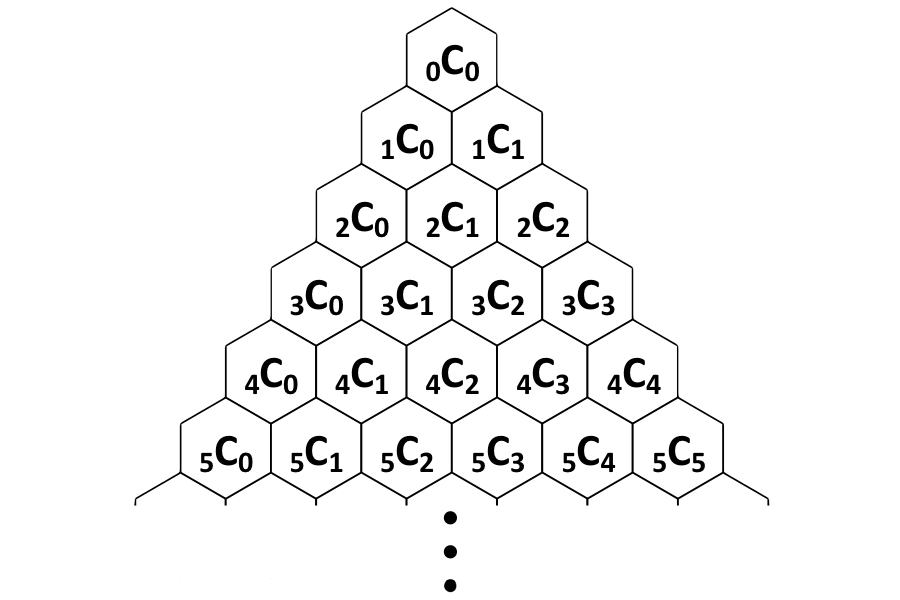
- Three colors for a single poster: A case like this where order does not matter is called a combination. The number of possible combinations will always be a fraction of the number of possible permutations. For a case with five options where three will be chosen, this is expressed as 5C3 and calculated as 5!/[3! (5-3)!] = 5!/(3! × 2!) = 5 × 4 × 3 / (3 × 2 × 1) = 10
This second case is significant to Pascal’s triangle, because the values can be calculated as follows:
From the process of generating Pascal’s triangle, we see any number can be generated by adding the two numbers above. Mathematically, this is expressed as nCr = n-1Cr-1 + n-1Cr — this relationship has been noted by various scholars of mathematics throughout history.
The Binomial Theorem
Binomial is a word used in algebra that roughly means “two things added together.” The binomial theorem refers to the pattern of coefficients (numbers that appear in front of variables) that appear when a binomial is multiplied by itself a certain number of times. Mathematically, this is written as (x + y)n. Pascal’s triangle can be used to determine the expanded pattern of coefficients. The first few expanded polynomials are given below.
Get the world’s most fascinating discoveries delivered straight to your inbox.
| n | (x + y)n | Expanded Polynomial | Pascal's Triangle |
| 0 | (x + y)0 | 1 | 1 |
| 1 | (x + y)1 | 1x + 1y | 1,1 |
| 2 | (x + y)2 | 1x2 + 2xy + 1y2 | 1,2,1 |
| 3 | (x + y)3 | 1x3 + 3x2y + 3xy2 + 1y3 | 1,3,3,1 |
| 4 | (x + y)4 | 1x4 + 4x3y + 6x2y2 + 4xy3 + 1y4 | 1,4,6,4,1 |
| 5 | (x + y)5 | 1x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + 1y5 | 1,5,10,10,5,1 |
| ↓ | ↓ | ↓ | ↓ |
Using summation notation, the binomial theorem may be succinctly written as:
The Binomial Distribution
For a probabilistic process with two outcomes (like a coin flip) the sequence of outcomes is governed by what mathematicians and statisticians refer to as the binomial distribution. This also relates to Pascal’s triangle.
For example for three coin flips, there are 2 × 2 × 2 = 8 possible heads/tails sequences. When sorted into groups of “how many heads (3, 2, 1, or 0)”, each group is populated with 1, 3, 3, and 1 sequences, respectively. Notice how this matches the third row of Pascal’s Triangle. It’s been proven that this trend holds for all numbers of coin flips and all the triangle’s rows.
| Coin flips | Possible sequences of heads (H) or tails (T) | Pascal's Triangle |
| 1 | H T | 1 1 |
| 2 | HH HT TH TT | 1 2 1 |
| 3 | HHH HHT HTH THH HTT THT TTH TTT | 1 3 3 1 |
| 4 | HHHH HHHT HHTH HTHH THHH HHTT HTHT HTTH THHT THTH TTHH HTTT THTT TTHT TTTH TTTT | 1 4 6 4 1 |
| ↓ | ↓ | ↓ |
According to George E.P. Box in "Statistics for Experimenters" (Wiley, 1978), for large numbers of coin flips (above roughly 20), the binomial distribution is a reasonable approximation of the normal distribution, a fundamental “bell-curve” distribution used as a foundation in statistical analysis. This approximation significantly simplifies the statistical analysis of a great deal of phenomena.
A physical example of this approximation can be seen in a bean machine, a device that randomly sorts balls to bins based on how they fall over a triangular arrangement of pegs. Because a ball hitting a peg has an equal probability of falling to the left or right, the likelihood of a ball landing all the way to the left (or right) after passing a certain number of rows of pegs exactly matches the likelihood of getting all heads (or tails) from the same number of coin flips. After a sufficient number of balls have collected past a triangle with n rows of pegs, the ratios of numbers of balls in each bin are most likely to match the nth row of Pascal’s Triangle.
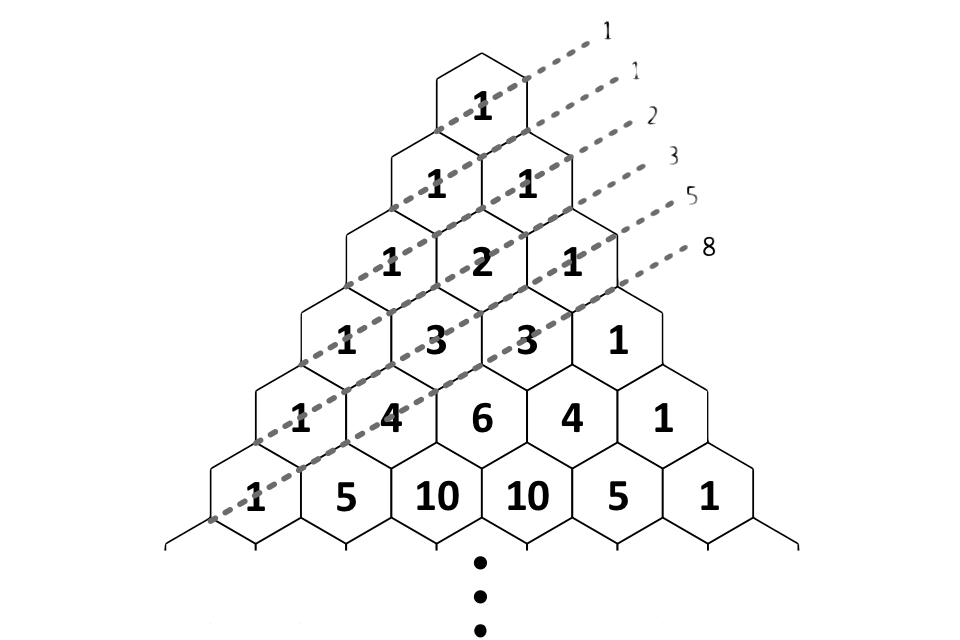
Fibonacci sequence
Pascal’s Triangle also has significant ties to number theory. The most apparent connection is to the Fibonacci sequence. Adding the numbers of Pascal’s triangle along a certain diagonal produces the numbers of the sequence.
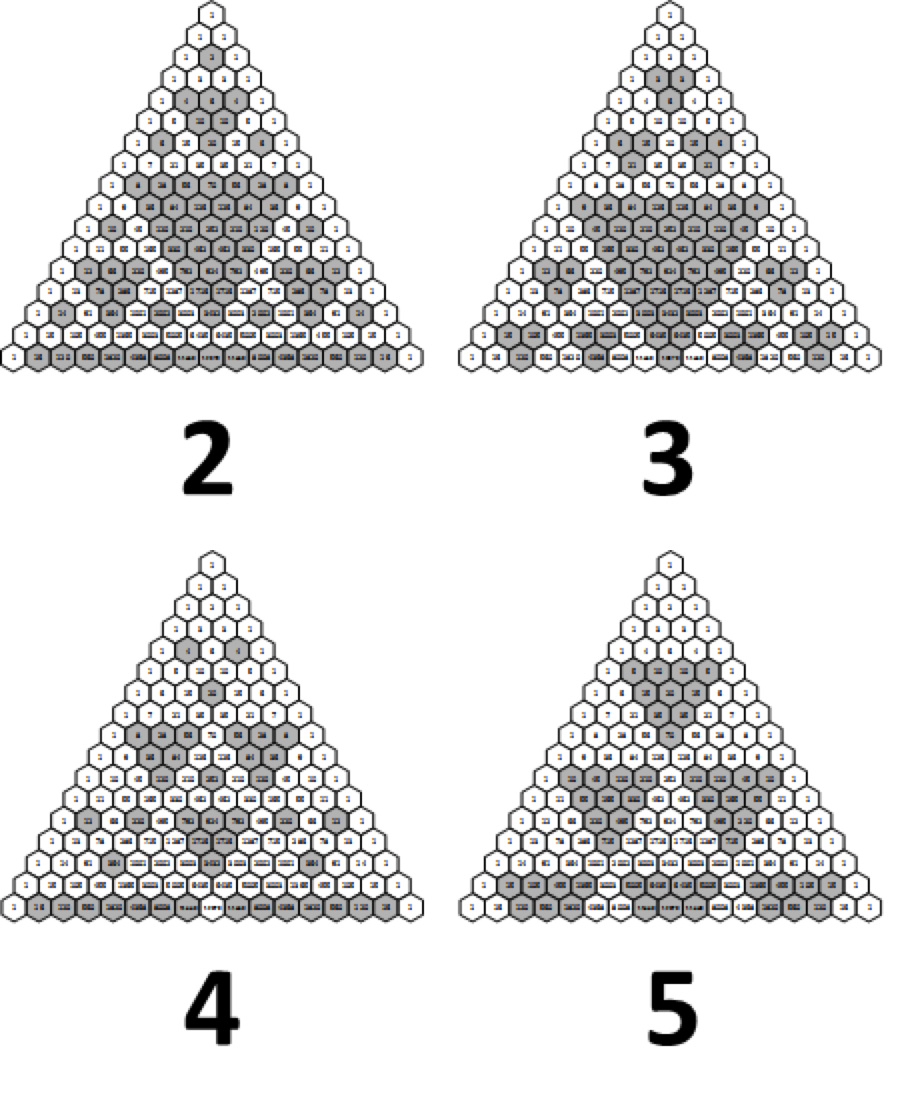
Fractals
Coloring the numbers of Pascal’s triangle by their divisibility produces an interesting variety of fractals. In particular, coloring all the numbers divisible by two (all the even numbers) produces the Sierpiński triangle. These patterns have appeared in Italian art since the 13th century, according to Wolfram MathWorld.
Additional resources
For more discussion about Pascal's triangle, go to:
Robert Coolman, PhD, is a teacher and a freelance science writer and is based in Madison, Wisconsin. He has written for Vice, Discover, Nautilus, Live Science and The Daily Beast. Robert spent his doctorate turning sawdust into gasoline-range fuels and chemicals for materials, medicine, electronics and agriculture. He is made of chemicals.