Mathematicians have uncovered a big new piece of evidence for one of the most famous unproven ideas in mathematics, known as the twin prime conjecture. But the route they took to finding that evidence probably won't help prove the twin prime conjecture itself.
The twin prime conjecture is all about how and when prime numbers — numbers that are divisible only by themselves and 1 — appear on the number line. "Twin primes" are primes that are two steps apart from each other on that line: 3 and 5, 5 and 7, 29 and 31, 137 and 139, and so on. The twin prime conjecture states that there are infinitely many twin primes, and that you'll keep encountering them no matter how far down the number line you go. It also states that there are infinitely many prime pairs with every other possible gap between them (prime pairs that are four steps apart, eight steps apart, 200,000 steps apart, etc.). Mathematicians are pretty sure this is true. It sure seems like it's true. And if it weren't true, it would mean that prime numbers aren't as random as everyone thought, which would mess up lots of ideas about how numbers work in general. But no one's ever been able to prove it.
Related: Mathematicians Edge Closer to Solving a 'Million Dollar' Math Problem
They might be closer now than ever before, though. In a paper published Aug. 12 in the preprint journal arXiv, as Quanta first reported, two mathematicians proved that the twin prime conjecture is true — at least in a sort of alternative universe.
This is what mathematicians do: work toward big proofs by proving smaller ideas along the way. Sometimes, the lessons learned from those smaller proofs can help with the bigger proof.
In this case, mathematicians Will Sawin of Columbia University and Mark Shusterman of the University of Wisconsin proved a version of the twin prime conjecture for the alternative universe of "finite fields": number systems that don't go to infinity like the number line, but instead loop back on themselves.
You probably encounter a finite field every day on the face of a clock. It goes 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and then loops back around to 1. In that finite field, 3+3 still equals 6. But 3+11=2.
Finite fields have polynomials, or expressions like "4x" or "3x+17x^2-4," Sawin told Live Science, just like regular numbers do. Mathematicians, he said, have learned that polynomials over finite fields behave a lot like integers — the whole numbers on the number line. Statements that are true about integers tend to also be trust about polynomials over finite fields, and vice-versa. And just like prime numbers come in pairs, polynomials come in pairs. For example, the twins of 3x+17x^2-4 are 3x+17x^2-2 and 3x+17x^2-6. And the nice thing about polynomials, Sawin said, is that unlike integers, when you plot them on a graph they make geometric shapes. For example, 2x+1 makes a graph that looks like this:
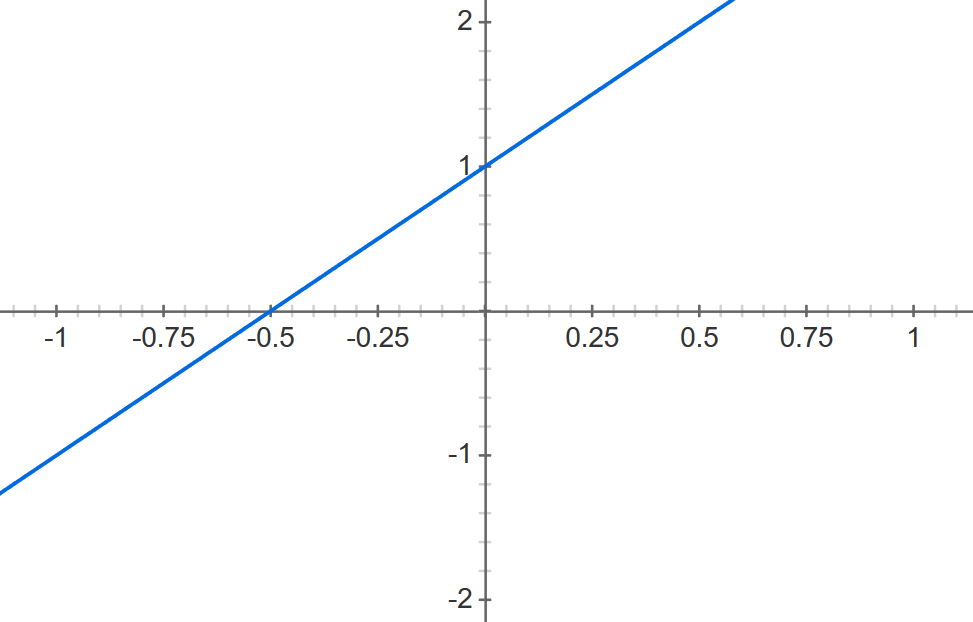
And 5x+x^2 makes a graph that looks like this:
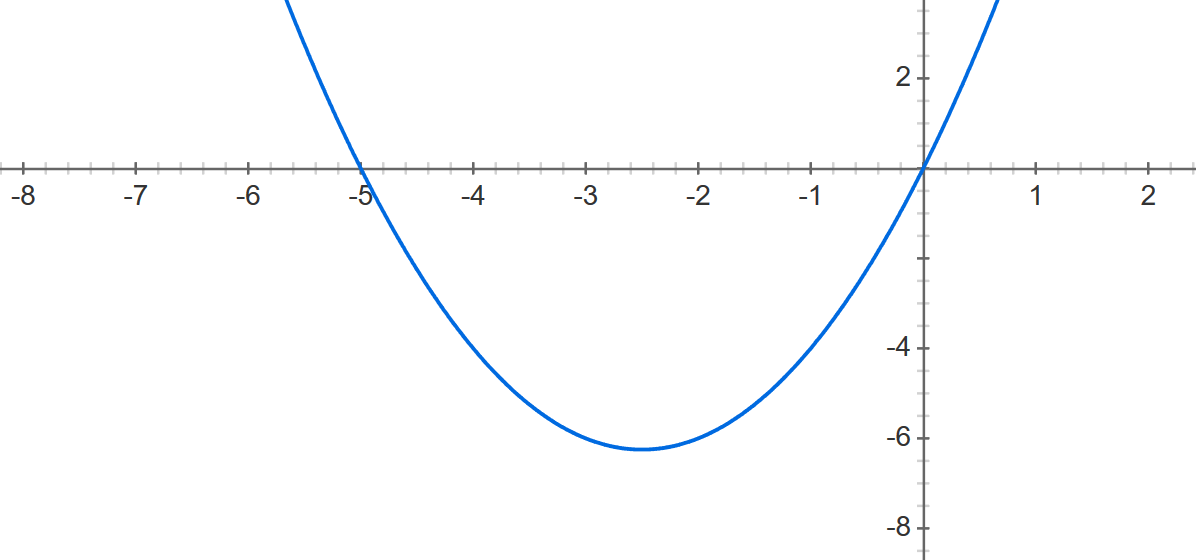
Because polynomials map out shapes, rather than the dots you get when you graph individual prime numbers, you can use geometry to prove things about polynomials that you can't prove about simple integers.
"We weren't the first people to notice that you can use geometry to understand finite fields," Shusterman told Live Science.
Other researchers had proven smaller versions of the twin primes hypothesis about certain kinds of polynomials over finite fields. But Sawin and Shusterman's proof required the researchers to go back and start from scratch in many respects, Sawin said.
"We had an observation that allowed us to perform a trick … that made the geometry much nicer so that it applies in all these cases," Shusterman said.
That geometric trick, he said led to their breakthrough: proving that this special version of the twin prime conjecture is true for all polynomials over finite fields, not just some of them.
The bad news, Sawin said, is that because their trick relies heavily on geometry, it probably won't be possible to use it to prove the twin prime conjecture itself. The underlying mathematics is just too different.
Still, Shusterman said, proving the finite fields case is a big new piece of evidence to add to the pile, teasing mathematicians with the possibility that the proof everyone's waiting for is out there somewhere.
It's as though they wanted to see the top of a tall steep mountain, and instead hauled their way up a different mountain nearby. They can almost see the distant peak, but it's shrouded in clouds. And the route they took to reach the top of the second mountain probably won't work on the mountain they're really interested in.
Shusterman said he hopes to keep working with Sawin on the twin primes problem, and that it's always possible something they learned in making this proof will turn out to be important to proving the twin prime conjecture after all.
- 9 Numbers That Are Cooler Than Pi
- The World's Most Beautiful Equations
- The 9 Most Massive Numbers in Existence
Originally published on Live Science.
