The Most Massive Numbers in Existence

Big numbers are everywhere, from the cells in the human body to the size of the universe. But once numbers edge past the realm of the physical, the human mind can struggle to grasp the sheer awesome scale of these numbers. Even infinity can seem easier to understand in comparison — it just goes on and on. And once numbers start to get large enough, everything starts to blur together, the late Jon Borwein, who was an applied mathematician at the University of Newcastle in Australia, told Live Science in 2013.

"We don't understand numbers on this scale," Borwein said.

From the humble trillion to Graham's number, here are some of the most mind-boggling numbers there are.

Big is relative

A map of the universe, with galaxies and stars, from Sloan Digital Sky Survey — This still from an animated fly-through of the new universe map created by the Sloan Digital Sky Survey-III shows the positions of galaxies mapped in 3D space. (Image credit: Miguel A. Aragón (Johns Hopkins University), Mark SubbaRao (Adler Planetarium), Alex Szalay (Johns Hopkins University), Yushu Yao (Lawrence Berkeley National Laboratory, NERSC), and the SDSS-III Collaboration)

When thinking about a personal budget, a $31.4 trillion debt ceiling is pretty inconceivable. But on the scale of the atoms in the universe, it looks absolutely paltry in comparison, Scott Aaronson, a computer scientist formerly at MIT and now at the University of Texas at Austin, told Live Science in 2013.

To try to understand huge numbers, most people rely on analogies of scale. For instance, Carl Sagan famously likened the age of the universe to a calendar year, with humans only showing up in the last few hours of New Year's Eve.

Riemann hypothesis

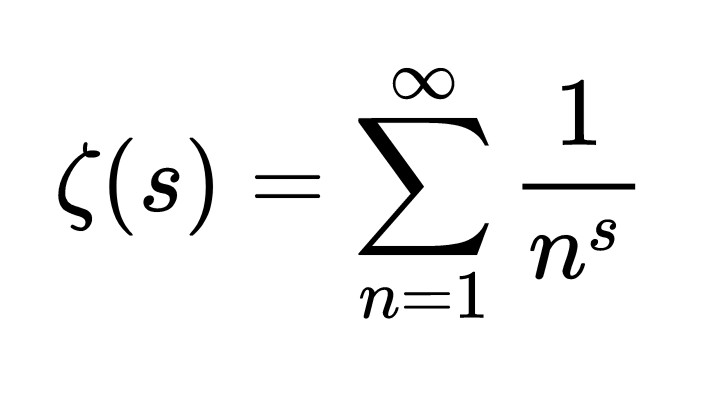
Riemanns Zeta function written out. — The Riemann zeta function. Anyone who solves the Riemann hypothesis, which states that any non-trivial zero of this equation is 1/2, will win a $1 million prize. (Image credit: Furfur)

First stated in 1859, the Riemann hypothesis is one of the greatest unsolved conjectures of mathematics, and whoever solves it will nab a $1 million prize. The hypothesis is that the real part of every non-trivial zero of a specific function, aptly named the Riemann zeta function, is 1/2.

"This is the biggest open question in mathematics, the one that will guarantee your name is known in 10,000 years," Borwein said.

The hypothesis, if true, has important implications for the distribution of prime numbers, which aren't divisible by anything other than themselves or one. To test the hypothesis, mathematicians look for extremely large primes — those bigger than about 10 raised to the power of 30, he said. That may sound abstract, but it has many real-world implications, Borwein said. "Primes are embedded in everything we use for encryption," he said. "That all relies on stuff where the algorithms are designed using properties of primes that we think are true but don't know."

The universe

An image of the farthest galaxy in a field of twinkling light taken by the James Webb telescope — NASA’s James Webb Space Telescope has produced the deepest and sharpest infrared image of the distant universe to date. The universe is thought to contain 10^ 82 atoms, research suggests. (Image credit: NASA, ESA, CSA, and STScI)

As far back as Archimedes, philosophers have wondered how many tiny particles could fit in the universe. Archimedes estimated that about 10 to the power of 63 grains of sand could fill the universe. He used a series of extremely rough estimates — the poppy seeds that make a grain of sand, the grains of sand that would cover the length of a stadium, and the stadia lengths between Earth and the sun, said Henry Mendell, a classical historian at California State University, Los Angeles.

Despite his crude measures, he wasn't too far off. Current estimates put the total number of atoms in the universe at about 10 to the 82.

Cosmological fudge factor

Abell galaxy cluster highlighted in purple light — The galaxy cluster Abell 1689. A study of Abell 1689 reveals something about how dark energy shapes the universe, a key element of the cosmological constant discrepancy. (Image credit: NASA, ESA, E. Jullo (JPL/LAM), P. Natarajan (Yale) and J-P. Kneib (LAM))

When Einstein conceived of his equations of relativity, he included a small constant, called the cosmological constant, to account for the fact that the universe is stationary. Though he later scrapped the constant when he learned the universe is expanding, it turns out the genius may have been on to something: Scientists believe the cosmological constant, which amounts to just 10 raised to the minus 122 power, reveals clues to the dark energy that is mysteriously accelerating the universe, Aaronson told Live Science in 2013.

The cosmological constant has been a huge headache for scientists because predictions differ from measurements of the constant by 120 orders of magnitude, and over the years, physicists have tried to explain away this discrepancy by tweaking other elements, such as how particle mass changes over time, Live Science previously reported.

Hercules and the Hydra

19th century illustration in ink of Hercules slaying a hydra — A 19th-century illustration of Hercules slaying the hydra. This myth inspired a riddle about how quickly the number of Hydra heads will grow if multiple sprout every time Hercules cuts off one. (Image credit: Getty Images)

Sometimes things have to get big before they get small. In 1982, mathematicians Jeff Paris and Laurie Kirby posed a riddle: Imagine Hercules fighting a Hydra that grows heads like a tree. If he cuts off one head, the mythic monster simply grows back a certain number of heads governed by a few rules. Amazingly, Hercules will always prevail against the Hydra eventually and chop off all of the Hydra's heads.

But even if Hercules is clever and chooses the most efficient strategy, the Hydra will first grow more than a googolplex of heads (or 10 raised to the power of 10 raised to the 100 power).

Mersenne primes

Woodcut image of bearded, balding monk Marin Mersenne — Marine Mersenne was a 17th century monk and polymath who is perhaps best known for describing a sequence of prime numbers, now named after him. (Image credit: ilbusca/Getty Images)

The Mersenne Primes are a class of numbers that get big in a hurry. These prime numbers are equal to 2 raised to the power of a prime number minus 1. While the first few start out small — 3, 7, 31 — they blow up to become incredibly large extremely quickly. Until about 1951, only 12 of these primes were known, but by this year (2024), 52 were known.

To power through these gigantic numbers, scientists use the Great Internet Mersenne Primes Search (GIMPS), which uses the computing power of thousands of Internet users to search for the elusive prime numbers. The largest known prime number was discovered in October 2024 by amateur researcher and former Nvidia employee Luke Durant. The number, 2^136,279,841 – 1, possesses a whopping 41,024,320 digits, more than 16 million digits more than the previous record holder, which was also discovered by GIMPS six years earlier.

A trillion triangles

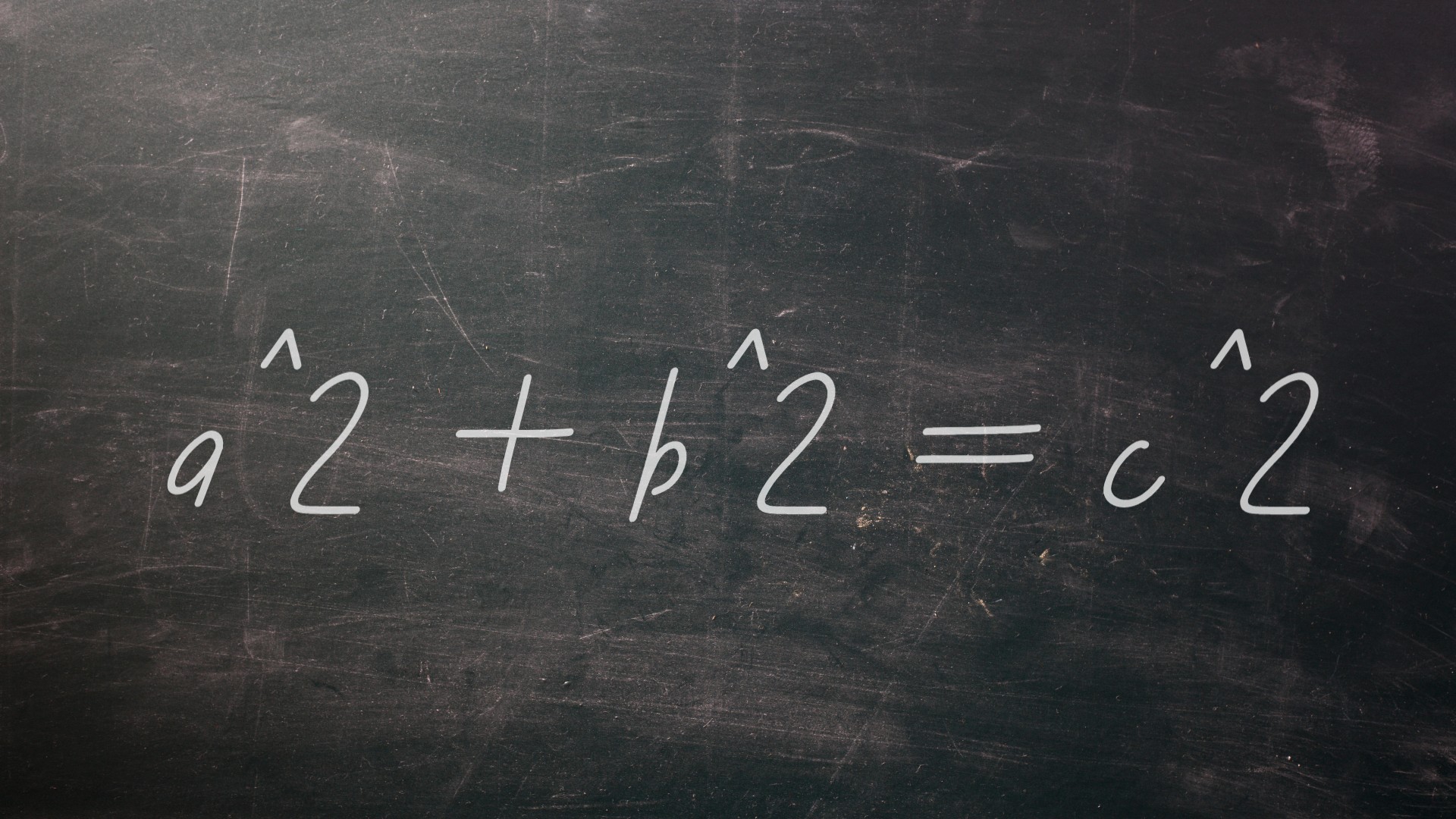
a^2+b^2=C^2 theorem written on a chalkboard — Right triangles in which the sides are all integers or fractions are known as congruent triangles, and the area of said triangles are known as congruent numbers. These numbers can get huge very, very quickly. (Image credit: Background: Eskay Lim / EyeEm via Getty Images)

Around 1000 years ago, Persian mathematician Al Karaji first asked how many congruent numbers existed. But just what are congruent numbers? The numbers are the area of right-angle triangles with integer or fraction length sides. So a triangle with sides of length of 3,4 and 5 would have an area of ½ * 3*4 = 6, making 6 a congruent number.

It took another millennia before the first hundred congruent numbers were discovered. By 2009, however supercomputers had discovered the first 3,148,379,694 congruent numbers. Some of these numbers are so enormous that if their digits were written out in decimal form, they would stretch to the moon and back. Gigantic numbers have interesting implications in data storage, because they are so huge that a stray gamma ray could disrupt the bits in these numbers and make them wrong, Borwein said.

Graham's number

Artist's concept of a supermassive black hole. — This illustration shows a black hole emitting jets of fast-moving plasma above and below it, as matter swirls around in an orbiting disk. (Image credit: NASA/JPL-Caltech)

All these numbers pale in comparison to Graham's number, a number so large that simply trying to remember all the digits would turn your head into a black hole. The number, which at one point was the largest number to ever be used in a math proof, arose in response to a simple riddle about how to allocate people to a certain set of committees with a few constraints.

While mathematicians are confident that at least 13 people are needed to solve the problem, in the 1970s mathematician and juggler Ronald Graham deduced that the number of people had to be lower than Graham's number. Simply computing the number would take 64 steps, and involves multiplying an insanely huge number of 3s.

There is no way to write the number out using scientific notation, and instead it must be written with a series of up-arrows that denote towers of exponents. Later on, Graham showed that the upper bound to for this riddle is much much smaller than Graham's number, but still huge.

TREE(3)

While Graham's number was one of the largest numbers proposed for a specific math proof, mathematicians have gone even bigger since then. In 1998 the logician Harvey Friedman of The Ohio State University proposed a riddle asking how long a sequence of letters needs to be given certain parameters of repeating stretches of letters. While the answer isn't infinite, it's absolutely massive.

The number Friedman derived, TREE(3), is calculated by creating increasingly massive towers of twos raised to the power of two using something called Ackerman functions. To give a sense of the scale, the fourth Ackerman functions involves raising two to the power of 65,536 twos. But TREE(3) is massively, massively larger than that — so massive that it makes Graham's number look like the tiniest fleck of dust in comparison.

"These higher levels of largeness blur, where one is unable to sense one level of largeness from another," Friedman wrote in his paper.

Editor's Note: This article was originally published in 2013 and updated on Nov. 17, 2023 to note new information on the largest prime, atoms in the observable universe and the cosmological constant. The article was updated again in Oct. 2024 after a new largest prime number was discovered.