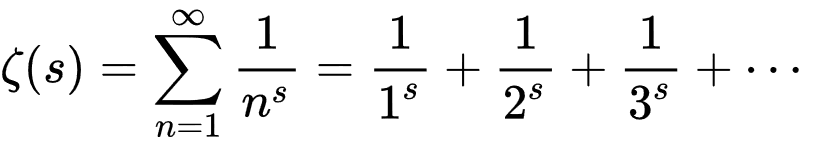Mathematicians Edge Closer to Solving a 'Million Dollar' Math Problem

Did a team of mathematicians just take a big step toward answering a 160-year-old, million-dollar question in mathematics?
Maybe. The crew did solve a number of other, smaller questions in a field called number theory. And in doing so, they have reopened an old avenue that might eventually lead to an answer to the old question: Is the Riemann hypothesis correct?
The Reimann hypothesis is a fundamental mathematical conjecture that has huge implications for the rest of math. It forms the foundation for many other mathematical ideas — but no one knows if it's true. Its validity has become one of the most famous open questions in mathematics. It's one of seven "Millennium Problems" laid out in 2000, with the promise that whoever solves them will win $1 million. (Only one of the problems has since been solved.) [5 Seriously Mind-Boggling Math Facts]
Where did this idea come from?
Back in 1859, a German mathematician named Bernhard Riemann proposed an answer to a particularly thorny math equation. His hypothesis goes like this: The real part of every non-trivial zero of the Riemann zeta function is 1/2. That's a pretty abstract mathematical statement, having to do with what numbers you can put into a particular mathematical function to make that function equal zero. But it turns out to matter a great deal, most importantly regarding questions of how often you'll encounter prime numbers as you count up toward infinity.
We'll come back to the details of the hypothesis later. But the important thing to know now is that if the Riemann hypothesis is true, it answers a lot of questions in mathematics.
"So often in number theory, what ends up happening is if you assume the Riemann hypothesis [is true], you're then able to prove all kinds of other results," Lola Thompson, a number theorist at Oberlin College in Ohio, who wasn't involved in this latest research, said.
Often, she told Live Science, number theorists will first prove that something is true if the Riemann hypothesis is true. Then they'll use that proof as a sort of stepping stone toward a more intricate proof, which shows that their original conclusion is true whether or not the Riemann hypothesis is true.
Get the world’s most fascinating discoveries delivered straight to your inbox.
The fact that this trick works, she said, convinces many mathematicians that the Riemann hypothesis must be true.
But the truth is that nobody knows for sure.
A small step toward a proof?
So how did this small team of mathematicians seem to bring us closer toward a solution?
"What we have done in our paper," said Ken Ono, a number theorist at Emory University and co-author of the new proof, "is we revisited a very technical criterion which is equivalent to the Riemann hypothesis … and we proved a large part of it. We proved a large chunk of this criterion."
A "criterion which is equivalent to the Riemann hypothesis," in this case, refers to a separate statement that is mathematically equivalent to the Riemann hypothesis.
It's not obvious at first glance why the two statements are so connected. (The criterion has to do with something called the "hyperbolicity of Jensen polynomials.") But in the 1920s, a Hungarian mathematician named George Pólya proved that if this criterion is true, then the Riemann hypothesis is true — and vice versa. It's an old proposed route toward proving the hypothesis, but one that had been largely abandoned.
Ono and his colleagues, in a paper published May 21 in the journal Proceedings of the Natural Academy of Sciences (PNAS), proved that in many, many cases, the criterion is true.
But in math, many is not enough to count as a proof. There are still some cases where they don't know if the criterion is true or false.
"It's like playing a million-number Powerball," Ono said. "And you know all the numbers but the last 20. If even one of those last 20 numbers is wrong, you lose. … It could still all fall apart."
Researchers would need to come up with an even more advanced proof to show the criterion is true in all cases, thereby proving the Riemann hypothesis. And it's not clear how far away such a proof is, Ono said.
So, how big a deal is this paper?
In terms of the Riemann hypothesis, it's tough to say how big a deal this is. A lot depends on what happens next.
"This [criterion] is just one of many equivalent formulations of the Riemann hypothesis," Thompson said.
In other words, there are a lot of other ideas that, like this criterion, would prove that the Riemann hypothesis is true if they themselves were proven.
"So, it's really hard to know how much progress this is, because on the one hand it's made progress in this direction. But, there's so many equivalent formulations that maybe this direction isn't going to yield the Riemann hypothesis. Maybe one of the other equivalent theorems instead will, if someone can prove one of those," Thompson said.
If the proof turns up along this track, then that will likely mean Ono and his colleagues have developed an important underlying framework for solving the Riemann hypothesis. But if it turns up somewhere else, then this paper will turn out to have been less important.
Still, mathematicians are impressed.
"Although this remains far away from proving the Riemann hypothesis, it is a big step forward," Encrico Bombieri, a Princeton number theorist who was not involved in the team's research, wrote in an accompanying May 23 PNAS article. "There is no doubt that this paper will inspire further fundamental work in other areas of number theory as well as in mathematical physics."
(Bombieri won a Fields Medal — the most prestigious prize in mathematics — in 1974, in large part for work related to the Riemann hypothesis.)
What does the Riemann hypothesis mean anyway?
I promised we'd get back to this. Here's the Riemann hypothesis again: The real part of every non-trivial zero of the Riemann zeta function is 1/2.
Let's break that down according to how Thompson and Ono explained it.
First, what's the Riemann zeta function?
In math, a function is a relationship between different mathematical quantities. A simple one might look like this: y = 2x.
The Riemann zeta function follows the same basic principles. Only it's much more complicated. Here's what it looks like.
It's a sum of an infinite sequence, where each term — the first few are 1/1^s, 1/2^s and 1/3^s — is added to the previous terms. Those ellipses mean the series in the function keeps going on like that, forever.
Now we can answer the second question: What is a zero of the Riemann zeta function?
This is easier. A "zero" of the function is any number you can put in for x that causes the function to equal zero.
Next question: What's the "real part" of one of those zeros, and what does it mean that it equals 1/2?
The Riemann zeta function involves what mathematicians call "complex numbers." A complex number looks like this: a+b*i.
In that equation, "a" and "b" stand for any real numbers. A real number can be anything from minus 3, to zero, to 4.9234, pi, or 1 billion. But there's another kind of number: imaginary numbers. Imaginary numbers emerge when you take the square root of a negative number, and they're important, showing up in all kinds of mathematical contexts. [10 Surprising Facts About Pi]
The simplest imaginary number is the square root of -1, which is written as "i." A complex number is a real number ("a") plus another real number ("b") times i. The "real part" of a complex number is that "a."
A few zeros of the Riemann zeta function, negative integers between -10 and 0, don't count for the Reimann hypothesis. These are considered "trivial" zeros because they’re real numbers, not complex numbers. All the other zeros are "non-trivial" and complex numbers.
The Riemann hypothesis states that when the Riemann zeta function crosses zero (except for those zeros between -10 and 0), the real part of the complex number has to equal to 1/2.
That little claim might not sound very important. But it is. And we may be just a teensy bit closer to solving it.
Originally published on Live Science.