5 Seriously Mind-Boggling Math Facts

Boring or Not?

Mathematics is one of the only areas of knowledge that can objectively be described as "true," because its theorems are derived from pure logic. And yet, at the same time, those theorems are often extremely strange and counter-intuitive.

Some people find math boring. As these examples show, it's anything but.

Random Patterns

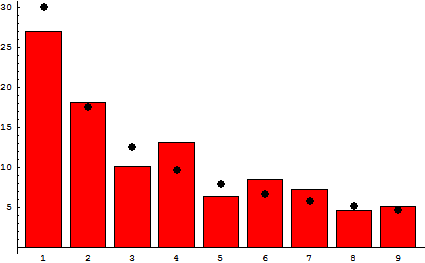
Weirdly, random data isn't actually all that random. In a given list of numbers representing anything from stock prices to city populations to the heights of buildings to the lengths of rivers, about 30 percent of the numbers will begin with the digit 1. Less of them will begin with 2, even less with 3, and so on, until only one number in twenty will begin with a 9. The bigger the data set, and the more orders of magnitude it spans, the more strongly this pattern emerges.

Latest Videos From

Watch full video here:

Prime Spirals

Because prime numbers are indivisible (except by 1 and themselves), and because all other numbers can be written as multiples of them, they are often regarded as the "atoms" of the math world. Despite their importance, the distribution of prime numbers among the integers is still a mystery. There is no pattern dictating which numbers will be prime or how far apart successive primes will be.

The seeming randomness of the primes makes the pattern found in "Ulam spirals" very strange indeed.

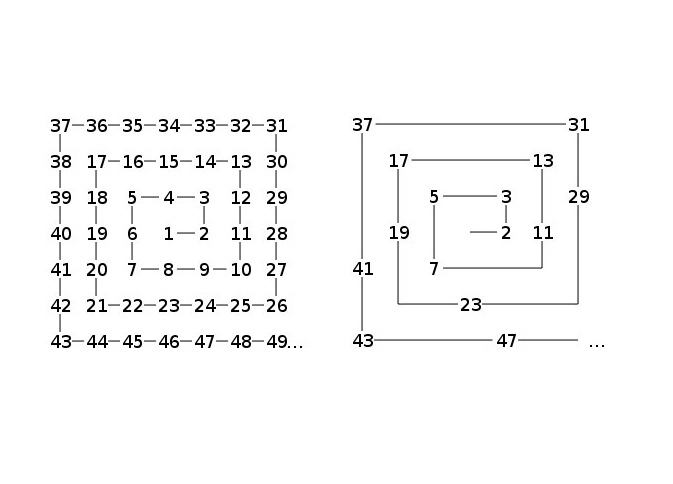
In 1963, the mathematician Stanislaw Ulam noticed an odd pattern while doodling in his notebook during a presentation: When integers are written in a spiral, prime numbers always seem to fall along diagonal lines. This in itself wasn't so surprising, because all prime numbers except for the number 2 are odd, and diagonal lines in integer spirals are alternately odd and even. Much more startling was the tendency of prime numbers to lie on some diagonals more than others — and this happens regardless of whether you start with 1 in the middle, or any other number.

Even when you zoom out to a much larger scale, as in the plot of hundreds of numbers below, you can see clear diagonal lines of primes (black dots), with some lines stronger than others. There are mathematical conjectures as to why this prime pattern emerges, but nothing has been proven.

Sphere Eversion

{youtube I6cgca4Mmcc&feature=related}

In an important field of mathematics called topology, two objects are considered to be equivalent, or "homeomorphic," if one can be morphed into the other by simply twisting and stretching its surface; they are different if you have to cut or crease the surface of one to reshape it into the form of the other.

Consider, for example, a torus — the dougnut-shape object shown in the intro slide. If you turn it upright, widen one side and indent the top of that side, you then have a cylindrical object with a handle. Thus, a classic math joke is to say that topologists can't tell their doughnuts from their coffee cups.

On the other hand, Moebius bands — loops with a single twist in them — are not homeomorphic with twist-free loops (cylinders), because you can't take the twist out of a Moebius band without cutting it, flipping over one of the edges, and reattaching.

Topologists long wondered: Is a sphere homeomorphic with the inside-out version of itself? In other words, can you turn a sphere inside out? At first it seems impossible, because you aren't allowed to poke a hole in the sphere and pull out the inside. But in fact, "sphere eversion," as it's called, is possible. Watch the video above to see how it's done.

Incredibly, the topologist Bernard Morin, a key developer of the complex method of sphere eversion shown here, was blind.

Wall Math

Though they may be decorated with an infinite variety of flourishes, mathematically speaking, there's just a finite number of distinct geometric patterns. All Escher paintings, wallpapers, tile designs and indeed all two-dimensional, repeating arrangements of shapes can be identified as belonging to one or another of the so-called "wallpaper groups." And how many wallpaper groups are there? Exactly 17. [How Do Calculators Calculate?]

The Sonnet

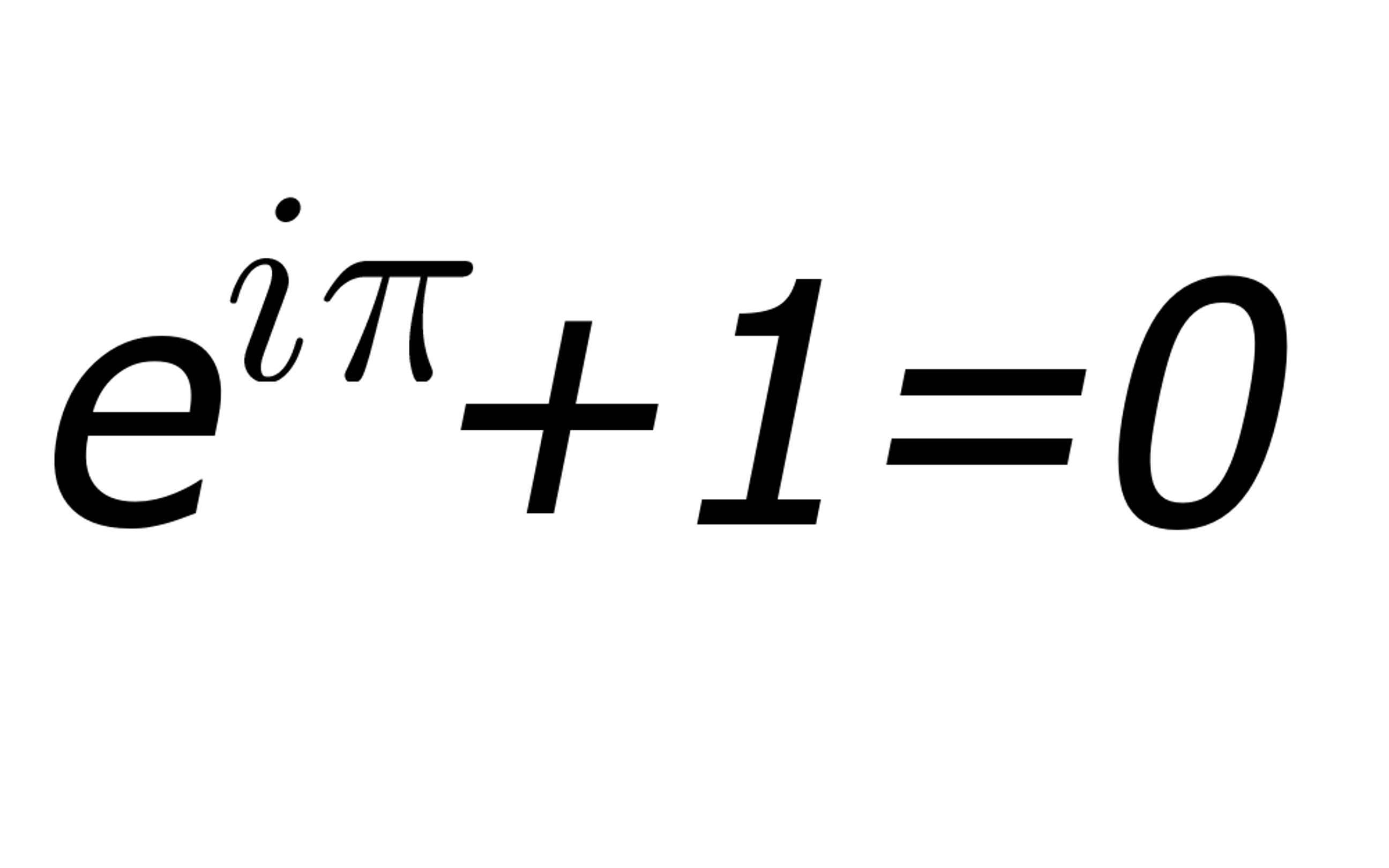
"Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's Equation reaches down into the very depths of existence."

Stanford mathematician Keith Devlin wrote these words about the equation to the left in a 2002 essay called "The Most Beautiful Equation." But why is Euler's formula so breath-taking? And what does it even mean?

First, the letter "e" represents an irrational number (with unending digits) that begins 2.71828... Discovered in the context of continuously compounded interest, it governs the rate of exponential growth, from that of insect populations to the accumulation of interest to radioactive decay. In math, the number exhibits some very surprising properties, such as — to use math terminology — being equal to the sum of the inverse of all factorials from 0 to infinity. Indeed, the constant "e" pervades math, appearing seemingly from nowhere in a vast number of important equations.

Next, "i" represents the so-called "imaginary number": the square root of negative 1. It is thus called because, in reality, there is no number which can be multiplied by itself to produce a negative number (and so negative numbers have no real square roots). But in math, there are many situations where one is forced to take the square root of a negative. The letter "i" is therefore used as a sort of stand-in to mark places where this was done.

Pi, the ratio of a circle's circumference to its diameter, is one of the best-loved and most interesting numbers in math. Like "e," it seems to suddenly arise in a huge number of math and physics formulas. What Makes Pi So Special?]

Putting it all together, the constant "e" raised to the power of the imaginary "i" multiplied by pi equals -1. And, as seen in Euler's equation, adding 1 to that gives 0. It seems almost unbelievable that all these strange numbers — and even one that isn't real — would combine so simply. But it's a proven fact.