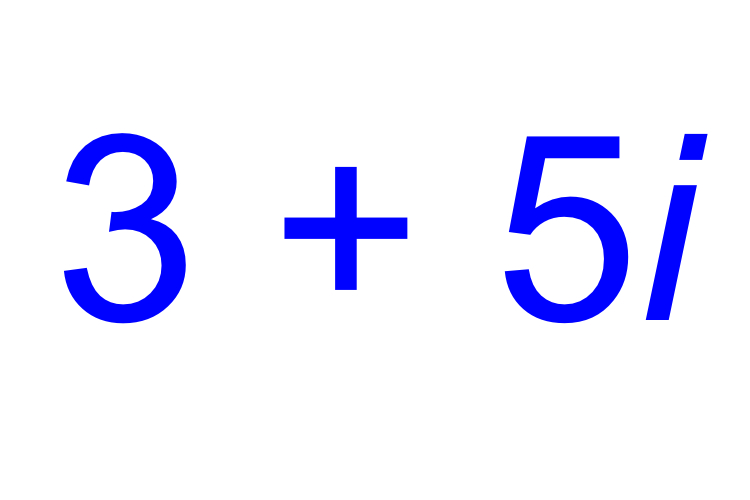
Complex numbers are numbers that consist of two parts — a real number and an imaginary number. Complex numbers are the building blocks of more intricate math, such as algebra. They can be applied to many aspects of real life, especially in electronics and electromagnetism.
The standard format for complex numbers is a + bi, with the real number first and the imaginary number last. Because either part could be 0, technically any real number or imaginary number can be considered a complex number. Complex does not mean complicated; it means that the two types of numbers combine to form a complex, like a housing complex — a group of buildings joined together.
Real numbers are tangible values that can be plotted on a horizontal number line, such as fractions, integers or any countable number that you can think of. Imaginary numbers are abstract concepts that are used when you need the square root of a negative number.
Adding & multiplying complex numbers
Because a complex number is a binomial — a numerical expression with two terms — arithmetic is generally done in the same way as any binomial, by combining the like terms and simplifying. For example:
(3 + 2i) + (4 - 4i)
(3 + 4) = 7
(2i - 4i) = -2i
The result is 7-2i.
For multiplication, you employ the FOIL method for polynomial multiplication: multiply the First, multiply the Outer, multiply the Inner, multiply the Last, and then add. For example:
(3 - 2i)(5 + 3i) =
(3)(5) + (3)(3i) + (-2i)(5) + (-2i)(3i) =
15 + 9i + -10i + -6i2 =
15 - i - 6(-1) =
21 - i
The reason that i2 simplifies to (-1) is because i is the square root of -1.
Dividing complex numbers
Division, however, becomes more complicated and requires using conjugates. Complex conjugates are pairs of complex numbers that have different signs, such as (a + bi) and (a - bi). Multiplying complex conjugates causes the middle term to cancel out. For example:
(a + bi)(a - bi) = a2 - abi + abi - (bi)2
This simplifies to a2 - b2(i2) = a2 - b2(-1)
The final result is a2 + b2
When dividing complex numbers, determine the conjugate of the denominator and multiply the numerator and denominator by the conjugate. For example,
(5 + 2i) ÷ (7 + 4i)
The conjugate of 7 + 4i is 7 - 4i. So, multiply the numerator and denominator by the conjugate:
(5 + 2i)(7 – 4i) ÷ (7 + 4i)(7 - 4i) =
(35 + 14i – 20i – 8i2) ÷ (49 - 28i + 28i – 16i2 ) =
(35 - 6i + 8) ÷ (49 + 16) =
(43 - 6i) ÷ 65
Absolute value of complex numbers
The absolute value of a number is considered its distance from zero on the number line. Because complex numbers include imaginary numbers, they cannot be plotted on the real number line. However, they can be measured from zero on the complex number plane, which includes an x axis (for the real number) and the y axis (for the imaginary number).
Uses of complex numbers
Complex numbers can be used to solve quadratics for zeroes. The quadratic formula solves ax2 + bx + c = 0 for the values of x. If the formula provides a negative in the square root, complex numbers can be used to simplify the zero.
Complex numbers are used in electronics and electromagnetism. A single complex number puts together two real quantities, making the numbers easier to work with. For example, in electronics, the state of a circuit element is defined by the voltage (V) and the current (I). Circuit elements can also have a capacitance (c) and inductance (L) that describes the circuit's tendency to resist changes in V and I. Rather than describing the circuit element's state by V and I, it can be described as z = V + Ii. The laws of electricity can then be expressed using the addition and multiplication of complex umbers.
As mentioned before, this can also be applied to electromagnetism. Instead of being described as electric field strength and magnetic field strength, you can create a complex number where the electric and magnetic components are the real and imaginary numbers.
