What Is a Proof?

A proof is a rigorous argument that shows a mathematical claim to be true.

Mathematics is different from other fields of science because claims are held to a different standard. Using the scientific method, claims are tested in order to verify or debunk them. Any person can do rigorous experiments to verify, for example, that the Earth is round or that lightning is electricity. No rigorous experiment has yet been able to disprove these claims (and likely none ever will). This standard of empiricism continues to shed light on countless untold secrets of the universe; however, it is surprisingly un-powerful in the field of mathematics.

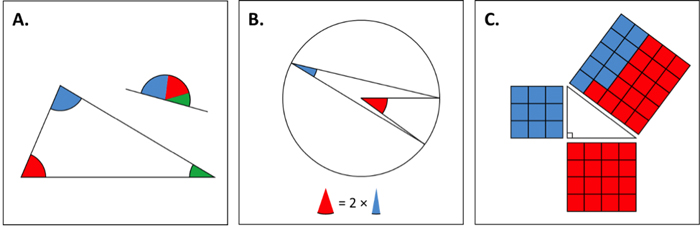
In math, it is not enough to merely do experiments on claims in order to validate their truth; one must also show they are true in every case. Mathematicians accomplish this by thinking up proofs. Take the following claims as examples:

Latest Videos From

Watch full video here:

1. The angles of a triangle add up to a straight line
2. The measure of a central angle is twice that of a circumscribed angle which shares the same arc
3. The sum of the squares of the legs of a triangle equal the square of that triangle’s hypotenuse

Each diagram serves as an experiment of each claim, but by no means proves them because each experiment only shows the claim true for one case each. Maybe we got lucky — just because a claim works for one case doesn’t mean it’s going to work for all of them. We might be able to strengthen the case if we do more examples, but this isn’t how mathematics works, and for a good reason. To prove something in mathematics, we have to show it’s true for every case. Yes. Every single possible case. 

Let’s take a moment to think how strong these claims are by exploring claim (C) in more detail. Today, we call this the Pythagorean Theorem in honor of the ancient Greek mathematician Pythagoras. Sometimes this is written as the equation a2 + b2 = c2, in which a and b are the legs, and c is the hypotenuse — the side opposite the right angle. The claim is that every right triangle you ever draw or find in nature will always have this property. It doesn’t matter if you’re here on Earth now, or on some alien planet 10,000 years in the future. Every possible right triangle ever, no matter the length of the sides, will work. Now, forever and always.

Not convinced? This would be a claim easy enough to disprove; all you’d have to do is find just one right triangle that violates the rule. You could spend hours, days, or years drawing and measuring right triangles in the hopes that you’ll stumble on just one example that violates Pythagoras’ theorem. You’d be famous if you found just one violation. Just one! You’d be wasting your time though, and we know this because the Pythagorean Theorem has been proved. We can be sure about the absoluteness of our claims because in many ways, mathematical proofs are even more powerful than scientific experimentation.

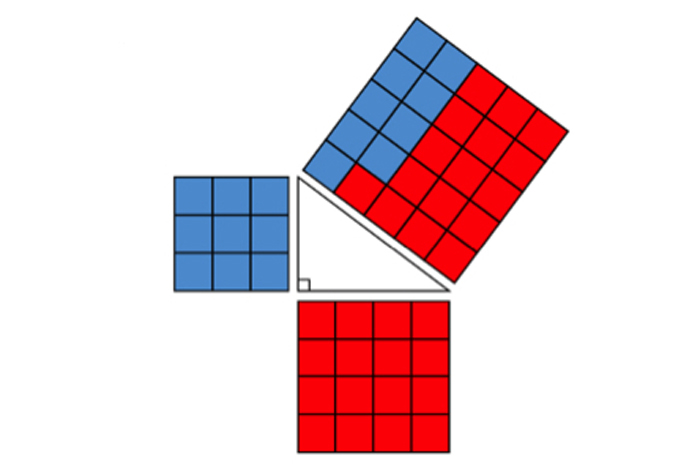
Rather than drawing and measuring every possible triangle, which would be impossible (it would literally take forever) we have to be more creative. Consider the following series of diagrams:

In Diagram 1, we have four copies of a right triangle. If we arrange them in a square so that the right angles form the four corners of a square, the square that forms in the middle space happens to be the square of the triangle’s hypotenuse (c²). If we rearrange two of the triangles (Diagram 2), we see that two squares are created (Diagram 3), each one having the area of the square of each of the triangle’s legs (a² + b²). From this rearrangement, it’s clear that the square of any right triangle’s hypotenuse is the sum of the squares of that triangle's legs. Taking a moment to realize this procedure works for every possible right triangle, it becomes clear that this short exercise proves the Pythagorean Theorem. That it has been proven is how we know we’ll never find a right triangle that violates the Pythagorean Theorem.

This property of right triangles was known long before the time of Pythagoras. Babylonian tablets dated to about 1750 B.C. contain lists of right triangles with whole-number lengths (what are now referred to as “Pythagorean Triples”). The presence of these lists suggests that people had long suspected that all right triangles possess the property described in the Pythagorean Theorem. In modern times, we call this a conjecture; a mathematical claim we suspect to be true, but not yet proven. A conjecture is similar to a hypothesis in the other sciences; basically an "educated guess." 

Why Pythagoras deserves special distinction is that he wrote the first known proof in the sixth century B.C., thus turning the conjecture into a theorem. Examples of modern conjectures include the Twin Prime Conjecture and the Riemann Hypothesis. Fame and fortune awaits those who can prove these conjectures that have outwitted generations of mathematicians. 

Why are we able to make such strong claims in mathematics? Arguably, it’s because we have the luxury of defining things so rigidly. In mathematics and logic, this is called formalism. We can be very specific about what does and does not constitute say, a right triangle, and are thus able to make very strong claims about the properties of these identifiers.

For example, take an orange and draw a right triangle on it. While such an act seems trivial by any reasonable standard of everyday speech, it turns out this is impossible. A right triangle, as we’ve thus far described it, must be flat. While we can easily draw a shape that resembles a right triangle, it will lack properties we’ve thus far identified in true (flat) right triangles. If you were to measure the sides of your pseudo right triangle, you’ll find that the square of the “hypotenuse” is less than the sum of the squares of the “legs.”

That we demand a right triangle be flat before proving the Pythagorean Theorem is what mathematicians call an axiom or postulate. “Axiom” comes from Greek ἀξίωμα (āxīoma) for “that which commends itself as evident.” We now call these “logical axioms”; one such example is “all right angles are equal to one another.” In modern times, it is understood that any system of formalism needs a fundamental set of assumed rules, thus non-logical axioms — those that is not a self-evident truths — are formal logical statements used as a basis upon which a mathematical theory is built. The non-logical axiom under which a right triangle is assumed to be flat is known as the “parallel postulate.” Basically, on a flat surface, parallel lines remain the same distance from each other forever until infinity. The same can’t be said for the surface of an orange or something saddle-shaped like a potato chip.

Geometry on flat surfaces is known as “Euclidean” after a geometry textbook writer of third century B.C. Greece. Staring about 1813, mathematicians such as Carl Friedrich Gauss (and later Bernhard Riemann) realized that mathematics need not be confined to describing flat geometries. This work became hugely important as it laid the groundwork for Einstein’s 1915 theory of general relativity, which describes the curvature of the fabric of space-time.

Robert Coolman is a graduate researcher at the University of Wisconsin-Madison, finishing up his Ph.D. in chemical engineering. He writes about math, science and how they interact with history. Follow Robert @PrimeViridian. Follow us @LiveScience, Facebook & Google+.