Euler’s Identity: 'The Most Beautiful Equation'
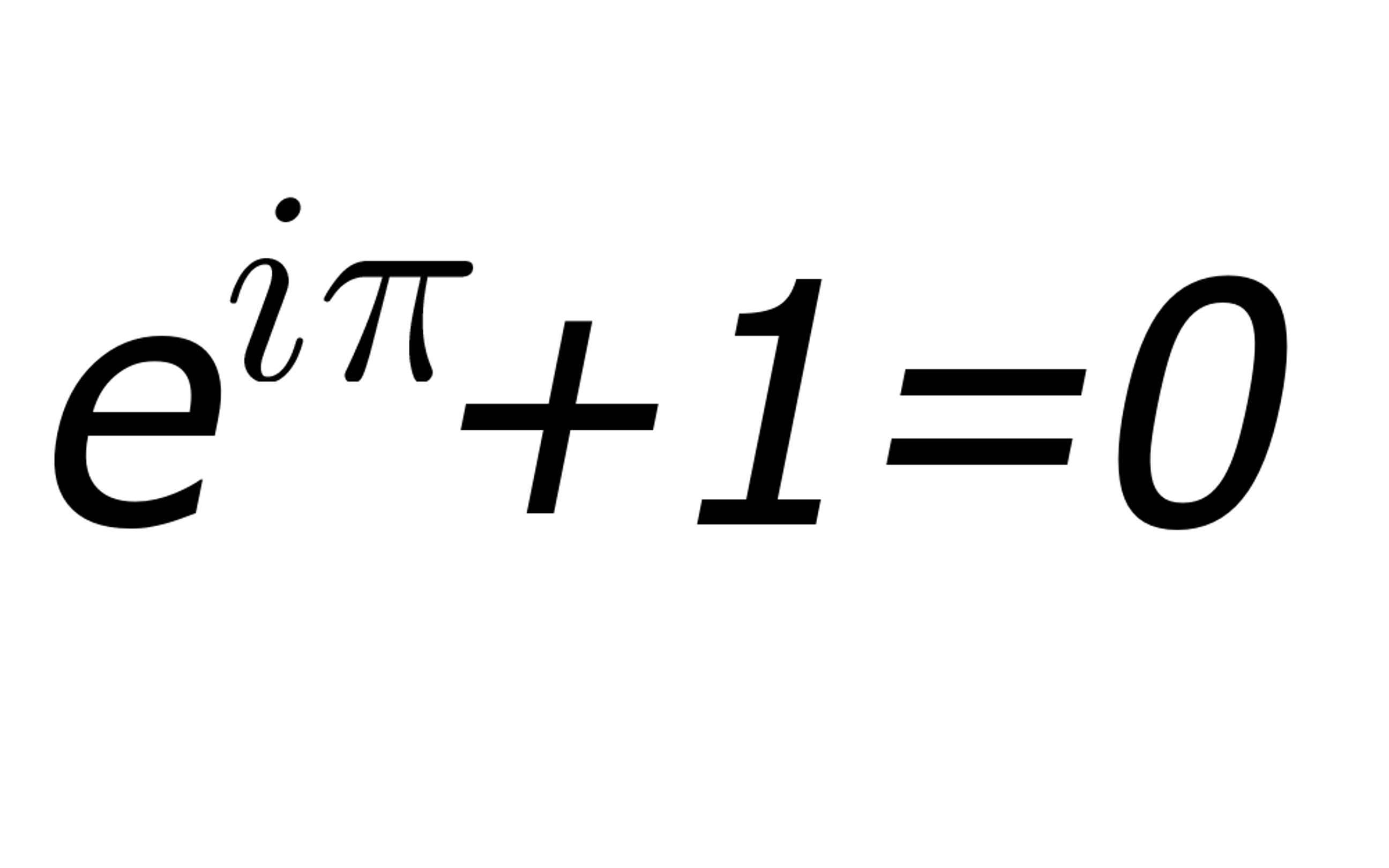
Euler’s identity is an equality found in mathematics that has been compared to a Shakespearean sonnet and described as "the most beautiful equation." It is a special case of a foundational equation in complex arithmetic called Euler’s Formula, which the late great physicist Richard Feynman called in his lectures "our jewel" and "the most remarkable formula in mathematics."
In an interview with the BBC, Prof David Percy of the Institute of Mathematics and its Applications said Euler's Identity was “a real classic and you can do no better than that … It is simple to look at and yet incredibly profound, it comprises the five most important mathematical constants.”
Euler's Identity is written simply as: eiπ + 1 = 0
The five constants are:
- The number 0.
- The number 1.
- The number π, an irrational number (with unending digits) that is the ratio of the circumference of a circle to its diameter. It is approximately 3.14159…
- The number e, also an irrational number. It is the base of natural logarithms that arises naturally through study of compound interest and calculus. The number e pervades math, appearing seemingly from nowhere in a vast number of important equations. It is approximately 2.71828….
- The number i, defined as the square root of negative one: √(-1). The most fundamental of the imaginary numbers, so called because, in reality, no number can be multiplied by itself to produce a negative number (and, therefore, negative numbers have no real square roots). But in math, there are many situations where one is forced to take the square root of a negative. The letter i is therefore used as a sort of stand-in to mark places where this was done.
Prolific mathematician
Leonhard Euler was an 18th-century Swiss-born mathematician who developed many concepts that are integral to modern mathematics. He spent most of his career in St. Petersburg, Russia. He was one of the most prolific mathematicians of all time, according to the U.S. Naval Academy (USNA), with 886 papers and books published. Much of his output came during the last two decades of his life, when he was totally blind. There was so much work that the St. Petersburg Academy continued publishing his work posthumously for more than 30 years.
Euler's important contributions include Euler's Formula and Euler's Theorem, both of which can mean different things depending on the context. According to the USNA, in mechanics, there are "Euler angles (to specify the orientation of a rigid body), Euler's theorem (that every rotation has an axis), Euler's equations for motion of fluids, and the Euler-Lagrange equation (that comes from calculus of variations)."
Multiplying complex numbers
Euler’s Identity stems naturally from interactions of complex numbers which are numbers composed of two pieces: a real number and an imaginary number; an example is 4+3i. Complex numbers appear in a multitude of applications such as wave mechanics (a study within quantum mechanics) and design of circuits that use alternating current (a common practice in electrical engineering). Additionally, complex numbers (and their cousins, the hyper complex numbers) have a property that makes them especially useful for studying computer graphics, robotics, navigation, flight dynamics, and orbital mechanics: multiplying them together causes them to rotate. This property will help us understand the reasoning behind Euler’s Identity.
In the example below, five complex numbers are plotted on the complex plane and together form a “house shape.” The complex plane is similar to a number line, except that it’s two-dimensional. The horizontal direction represents the real numbers and the vertical axis represents imaginary numbers. Each house-shape complex number is multiplied by the complex number 4+3i and re-plotted (green arrow). [Related: What Are Complex Numbers?]
As can be seen, multiplying by 4+3i results in the house shape dilating (increasing in area and moving away from the origin 0+0i by the same amount) and rotating (becoming tilted by some angle). To show this is precisely the effect of multiplying by 4+3i, the effect of zooming in on the house five times and rotating by 36.9 degrees is also shown (red arrow). The exact same effect is produced.

Different amounts of dilation and rotation can produce the effects of multiplying by any number on the complex plane.
Polar form of complex numbers
The amount of rotation and dilation is determined by properties intrinsic to the number 4+3i, which, as seen in the figure below, is five units from the origin (r = 5) and forms an angle of 36.9 degrees with the horizontal axis (φ = 36.9°). These measurements are used in what is known as the polar form of a complex number (reiφ) as opposed to the normal rectangular form (a+bi).
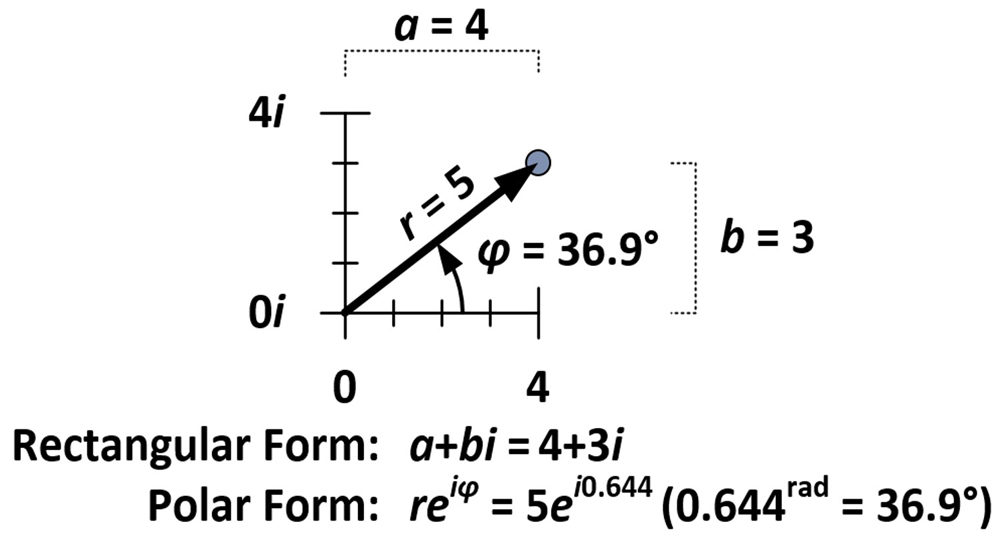
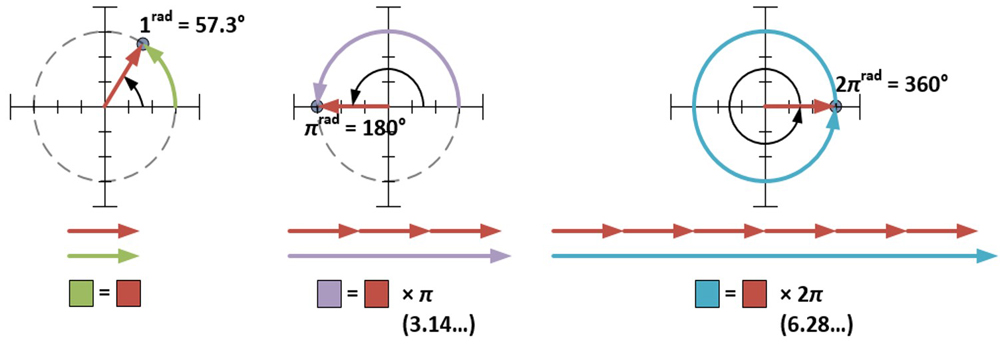
The polar form requires that φ be measured in radians. One radian (1rad) is approximately 57.3 degrees; it’s the measure of angle made when a circle’s radius is wrapped against that circle’s circumference. A measure of π radians wraps half way around a circle; a measure of 2π radians wraps a full circle.
The angle measure for 4+3i is 0.644 radians (36.9° = 0.644rad) meaning the polar form of 4+3i is 5ei0.644. Measures for r and φ can also be determined for each of the house-shape points, and yet another way of achieving the dilating/rotating effect of multiplying by 4+3i is to multiply each r by five, and add 36.9 degrees (or 0.644rad) to each φ. From this demonstration, we see that when complex numbers are multiplied together, distances multiply and angles add. This is due to a property intrinsic to exponents, which can be shown algebraically.
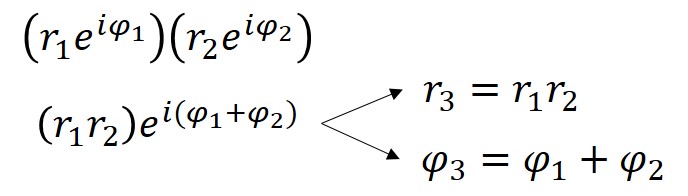
With the polar form of complex numbers established, the matter of Euler’s Identity is merely a special case of a+bi for a = -1 and b = 0. Consequently for the polar form reiφ, this makes r= 1 and φ = π (since πrad = 180°).
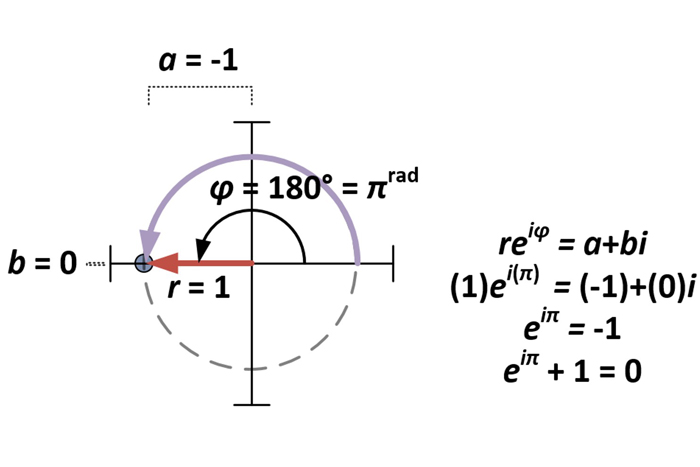
Derivation of polar form
Though Euler’s Identity follows from the polar form of complex numbers, it is impossible to derive the polar form (in particular the spontaneous appearance of the number e) without calculus.
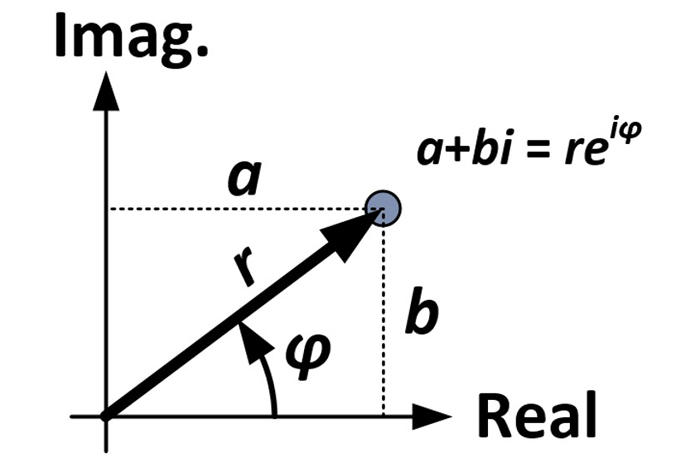
We start with the rectangular form of a complex number:
a + bi
From the diagram and trigonometry, we can make the following substitutions:
(r·cosφ) + (r·sinφ)i
From here we can factor out r:
r·(cosφ + i·sinφ)
Sometimes “cosφ + i·sinφ” is named cisφ, which is shorthand for “cosine plus imaginary sine.”
r·cisφ
The function cisφ turns out to be equal to eiφ. This is the part that’s impossible to show without calculus. Two derivations are shown below:

Thus, the equation r·cisφ is written in standard polar form r·eiφ.
Additional resources
Get the world’s most fascinating discoveries delivered straight to your inbox.
Robert Coolman, PhD, is a teacher and a freelance science writer and is based in Madison, Wisconsin. He has written for Vice, Discover, Nautilus, Live Science and The Daily Beast. Robert spent his doctorate turning sawdust into gasoline-range fuels and chemicals for materials, medicine, electronics and agriculture. He is made of chemicals.
