What Is Trigonometry?

Trigonometry is a branch of mathematics that studies relationships between the sides and angles of triangles. Trigonometry is found all throughout geometry, as every straight-sided shape may be broken into as a collection of triangles. Further still, trigonometry has astoundingly intricate relationships to other branches of mathematics, in particular complex numbers, infinite series, logarithms and calculus.
The word trigonometry is a 16th-century Latin derivative from the Greek words for triangle (trigōnon) and measure (metron). Though the field emerged in Greece during the third century B.C., some of the most important contributions (such as the sine function) came from India in the fifth century A.D. Because early trigonometric works of Ancient Greece have been lost, it is not known whether Indian scholars developed trigonometry independently or after Greek influence. According to Victor Katz in “A History of Mathematics (3rd Edition)” (Pearson, 2008), trigonometry developed primarily from the needs of Greek and Indian astronomers.
An example: Height of a sailboat mast
Suppose you need to know the height of a sailboat mast, but are unable to climb it to measure. If the mast is perpendicular to the deck and top of the mast is rigged to the deck, then the mast, deck and rigging rope form a right triangle. If we know how far the rope is rigged from the mast, and the slant at which the rope meets the deck, then all we need to determine the mast’s height is trigonometry.
For this demonstration, we need to examine a couple ways of describing “slant.” First is slope, which is a ratio that compares how many units a line increases vertically (its rise) compared to how many units it increases horizontally (its run). Slope is therefore calculated as rise divided by run. Suppose we measure the rigging point as 30 feet (9.1 meters) from the base of the mast (the run). By multiplying the run by the slope, we would get the rise — the mast height. Unfortunately, we don’t know the slope. We can, however, find the angle of the rigging rope, and use it to find the slope. An angle is some portion of a full circle, which is defined as having 360 degrees. This is easily measured with a protractor. Let’s suppose the angle between the rigging rope and the deck is 71/360 of a circle, or 71 degrees.
We want the slope, but all we have is the angle. What we need is a relationship that relates the two. This relationship is known as the “tangent function,” written as tan(x). The tangent of an angle gives its slope. For our demo, the equation is: tan(71°) = 2.90. (We'll explain how we got that answer later.)
This means the slope of our rigging rope is 2.90. Since the rigging point is 30 feet from the base of the mast, the mast must be 2.90 × 30 feet, or 87 feet tall. (It works the same in the metric system: 2.90 x 9.1 meters = 26.4 meters.)
Sine, cosine and tangent
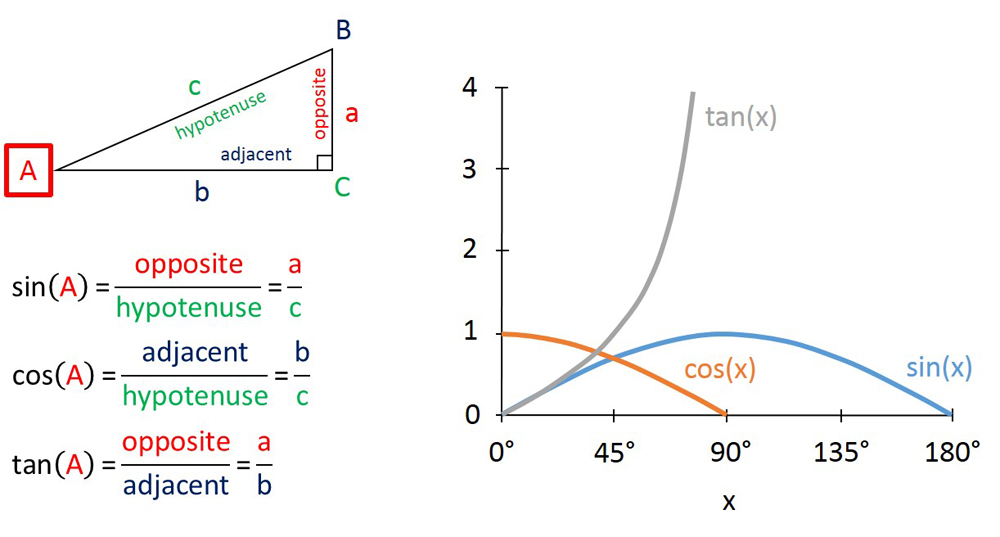
Depending on what is known about various side lengths and angles of a right triangle, there are two other trigonometric functions that may be more useful: the “sine function” written as sin(x), and the “cosine function” written as cos(x). Before we explain those functions, some additional terminology is needed. Sides and angles that touch are described as adjacent. Every side has two adjacent angles. Sides and angles that don’t touch are described as opposite. For a right triangle, the side opposite to the right angle is called the hypotenuse (from Greek for “stretching under”). The two remaining sides are called legs.
Get the world’s most fascinating discoveries delivered straight to your inbox.
Usually we are interested (as in the example above) in an angle other than the right angle. What we called “rise” in the above example is taken as length of the opposite leg to the angle of interest; likewise, the “run” is taken as the length of the adjacent leg. When applied to an angle measure, the three trigonometric functions produce the various combinations of ratios of side lengths.
In other words:
- The tangent of angle A = the length of the opposite side divided by the length of the adjacent side
- The sine of angle A = the length of the opposite side divided by the length of the hypotenuse
- The cosine of angle A = the length of the adjacent side divided by the length of the hypotenuse
From our ship-mast example before, the relationship between an angle and its tangent can be determined from its graph, shown below. The graphs of sine and cosine are included as well.
Worth mentioning, though beyond the scope of this article, is that these functions relate to each other through a great variety of intricate equations known as identities, equations that are always true.
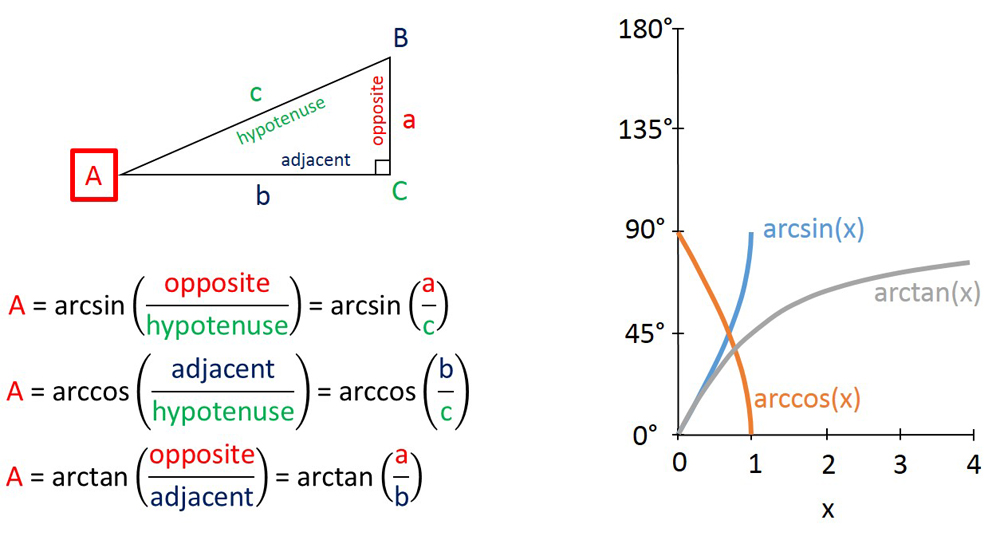
Each trigonometric function also has an inverse that can be used to find an angle from a ratio of sides. The inverses of sin(x), cos(x), and tan(x), are arcsin(x), arccos(x) and arctan(x), respectively.
Shapes other than right triangles
Trigonometry isn’t limited to just right triangles. It can be used with all triangles and all shapes with straight sides, which are treated as a collection of triangles. For any triangle, across the six measures of sides and angles, if at least three are known the other three can usually be determined. Of the six configurations of three known sides and angles, only two of these configurations can’t be used to determine everything about a triangle: three known angles (AAA), and a known angle adjacent and opposite to the known sides (ASS). Unknown side lengths and angles are determined using the following tools:
- The Law of Sines, which says that if both measures of one of the three opposing angle/side pairs are known, the others may be determined from just one known: sin(A)/a = sin(B)/b = sin(C)/c
- The Law of Cosines, which says that an unknown side can be found from two known sides and the angle between them. It’s essentially the Pythagorean Theorem with a correction factor for angles that aren’t 90 degrees: c2 = a2 + b2 – 2ab∙cos(C)
- The fact that all the angles in a triangle must add up to 180 degrees: A + B + C = 180°
The history of trigonometry
Trigonometry follows a similar path as algebra: it was developed in the ancient Middle East and through trade and immigration moved to Greece, India, medieval Arabia and finally Europe (where consequently, colonialism made it the version most people are taught today). The timeline of trigonometric discovery is complicated by the fact that India and Arabia continued to excel in the study for centuries after the passing of knowledge across cultural borders. For example, Madhava’s 1400 discovery of the infinite series of sine was unknown to Europe up through Isaac Newton’s independent discovery in 1670. Due to these complications, we’ll focus exclusively on the discovery and passage of sine, cosine, and tangent.
Beginning in the Middle East, seventh-century B.C. scholars of Neo-Babylonia determined a technique for computing the rise times of fixed stars on the zodiac. It takes approximately 10 days for a different fixed star to rise just before dawn, and there are three fixed stars in each of the 12 zodiacal signs; 10 × 12 × 3 = 360. The number 360 is close enough to the 365.24 days in a year but far more convenient to work with. Nearly identical divisions are found in the texts of other ancient civilizations, such as Egypt and the Indus Valley. According to Uta Merzbach in “A History of Mathematics” (Wiley, 2011), the adaptation of this Babylonian technique by Greek scholar Hypsicles of Alexandria around 150 B.C. was likely the inspiration for Hipparchus of Nicea (190 to 120 B.C.) to begin the trend of cutting the circle into 360 degrees. Using geometry, Hipparchus determined trigonometric values (for a function no longer used) for increments of 7.5 degrees (a 48th of a circle). Ptolemy of Alexandria (A.D. 90 to 168), in his A.D. 148 “Almagest”, furthered the work of Hipparchus by determining trigonometric values for increments of 0.5 degrees (a 720th of a circle) from 0 to 180 degrees.
The oldest record of the sine function comes from fifth-century India in the work of Aryabhata (476 to 550). Verse 1.12 of the “Aryabhatiya” (499), instead of representing angles in degrees, contains a list of sequential differences of sines of twenty-fourths of a right angle (increments of 3.75 degrees). This was the launching point for much of trigonometry for centuries to come.
The next group of great scholars to inherit trigonometry were from the Golden Age of Islam. Al-Ma'mun (813 to 833), the seventh caliph of the Abbasid Caliphate and creator of the House of Wisdom in Baghdad, sponsored the translation of Ptolemy’s "Almagest" and Aryabhata’s "Aryabhatiya" into Arabic. Soon after, Al-Khwārizmī (780 to 850) produced accurate sine and cosine tables in “Zīj al-Sindhind” (820). It is through this work that that knowledge of trigonometry first came to Europe. According to Gerald Toomer in the “Dictionary of Scientific Biography 7,” while the original Arabic version has been lost, it was edited around 1000 by al-Majriti of Al-Andalus (modern Spain), who likely added tables of tangents before Adelard of Bath (in South England) translated it into Latin in 1126.
Additional resources
Robert Coolman, PhD, is a teacher and a freelance science writer and is based in Madison, Wisconsin. He has written for Vice, Discover, Nautilus, Live Science and The Daily Beast. Robert spent his doctorate turning sawdust into gasoline-range fuels and chemicals for materials, medicine, electronics and agriculture. He is made of chemicals.