In geometry, an object exhibits symmetry if it looks the same after a transformation, such as reflection or rotation. Symmetry is the underlying mathematical principle behind all patterns and is important in art (used in architecture, pottery, quilting and rug making), mathematics (relating to geometry, group theory and linear algebra), biology (in shapes of organisms), chemistry (in shapes of molecules and crystal structures), and physics (where symmetries correspond to conserved quantities). The word "symmetry" is a 16th-century Latin derivative from the Greek words for "together" (syn-) and "measure" (metron).
Types of symmetry
Reflective
In general usage, symmetry most often refers to mirror or reflective symmetry; that is, a line (in 2-D) or plane (in 3-D) can be drawn through an object such that the two halves are mirror images of each other. An isosceles triangle and a human face are examples. Mathematically, an object that exhibits mirror symmetry is said to be “invariant under reflection,” meaning reflecting the object in a certain way doesn’t change its appearance.
In biology, reflective symmetry is often referred to as bilateral symmetry, as found in mammals, reptiles, birds and fish.
Rotational
Another form of symmetry commonly found in biology is radial symmetry. It is found in flowers and many sea creatures, such as sea anemones, sea stars and jellyfish. Mathematically, such objects are described as exhibiting rotational symmetry, for being “invariant under rotation.” Such objects have a point (in 2-D) or an axis (in 3-D) about which an object can be rotated some amount and remain invariant.
Translational
If imagined to extend for infinity in all directions, a 2-D or 3-D pattern can exhibit translational symmetry, for being “invariant under translation.” All tessellations, many jungle gyms and most patterns found on rugs and wallpaper exhibit translational symmetry.
Other forms of symmetry
While there are examples of objects that exhibit more than one type of symmetry (for example a six-pointed star exhibits six lines of reflection and a point of 6-fold rotation), there are some objects and patterns that are invariant only under two transformations done at the same time.
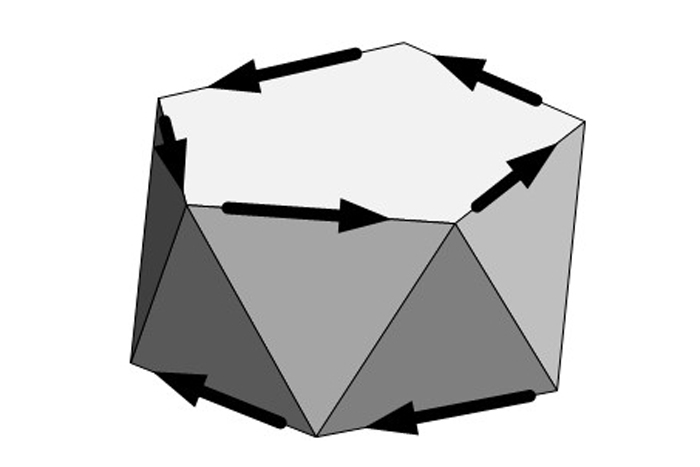
Improper Rotation = Reflection + Rotation
A pentagonal antiprism with directional edges is invariant under improper rotation (in the example above, rotation by a tenth of a circle, and reflected across a horizontal plane).
Glide Reflection = Translation + Reflection
A footprint pattern like the above example, if extended to infinity in either direction, is invariant under glide reflection (a translation combined with a reflection).
Screw Rotation = Translation + Rotation
A helix made of tetrahedrons, if extended to infinity in either direction, is invariant under screw rotation (in this example, a translation combined with a rotation of 131.8 degrees).
Categorizing objects and patterns
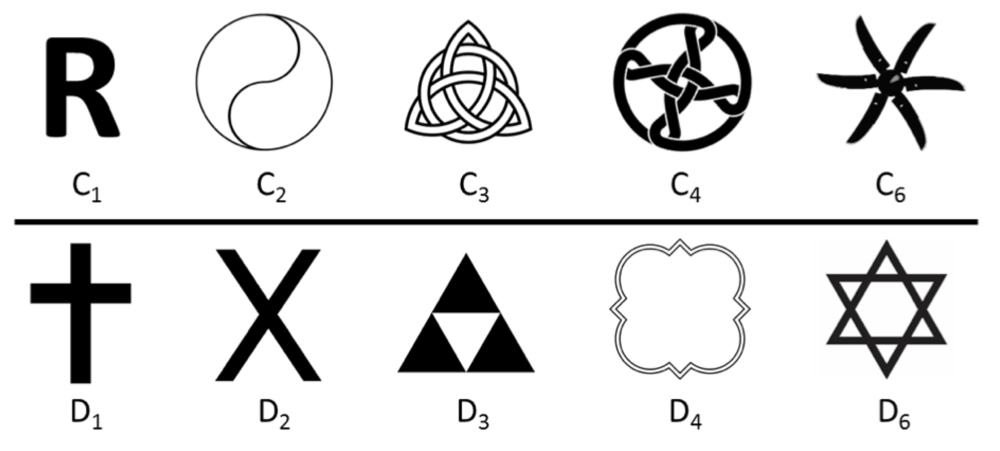
Mathematicians and crystallographers categorize an object’s or pattern’s symmetry according to the variety of ways it can be transformed and still remain invariant. A 2-D or 3-D object is assigned a "point group" to indicate all the ways it can remain invariant under reflection and rotation (and in 3-D, improper rotation). When using an object as a pattern motif, it is convenient to assign it to one of the crystallographic point groups: in 2-D, there are 10 of these (shown below); in 3-D, there are 32.
In common notation, called Schoenflies notation after Arthur Moritz Schoenflies, a German mathematician:
- “C” stands for “cyclic.” These objects have rotational symmetry, but no reflective symmetry. The number indicates what-fold rotational symmetry they have, so the symbol labeled C2 has two-fold symmetry, for example. All cyclic shapes have a mirror image that “spins the other way.”
- “D” stands for “dihedral.” These objects have both reflective and rotational symmetry. The number indicates what-fold rotational symmetry they have as well as the number of lines of symmetry.
Lattices
A lattice is a repeating pattern of points in space where an object can be repeated (or more precisely, translated, glide reflected, or screw rotated). In 1-D there’s just one lattice, in 2-D there are five, and in 3-D there are 14.
To make a pattern, a 2-D object (which will have one of the 10 crystallographic point groups assigned to it) is repeated along a 1-D or 2-D lattice. A 2-D object repeated along a 1-D lattice forms one of seven frieze groups. A 2-D object repeated along a 2-D lattice forms one of 17 wallpaper groups.
3-D patterns are more complicated, and are rarely found outside of crystallography. The various 3-D point groups repeated along the various 3-D lattices form 230 varieties of space group. 3-D objects can also be repeated along 1-D or 2-D lattices to produce rod groups or layer groups, respectively.
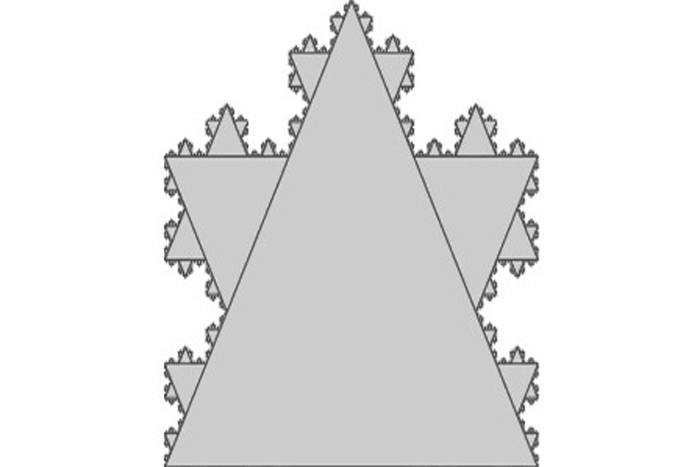
Fractals
Also important is invariance under a fourth kind of transformation: scaling. Concentric circles of geometrically progressing diameter are invariant under scaling. When an object is invariant under a specific combination of translation, reflection, rotation and scaling, it produces a new kind of pattern called a fractal.
Additional resources
- Symmetry: An open access journal covering research on symmetry phenomena wherever they occur in mathematical and scientific studies.
- Otterbein University: Symmetry Resources — to help students learn concepts of molecular symmetry and to help faculty teach concepts of molecular symmetry.
- Nanyang Technological University in Singapore offers an online course, "Beauty, Form & Function: An Exploration of Symmetry."
