Honeycombs, some bathroom floors and designs by artist M.C. Escher have something in common: they are composed of repeating patterns of the same shape without any overlaps or gaps. This type of pattern is called tiling, or tessellation.
The word "tessellate" means to form or arrange small squares in a checkered or mosaic pattern, according to Drexel University. It comes from the Greek tesseres, which means "four." The first tilings were made from square tiles. As an art form, tessellation is particularly rich in mathematics, with ties to geometry, topology and group theory. Cultures ranging from Irish and Arabic to Indian and Chinese have all practiced tiling at various levels of complexity. Let's explore the wide variety of tessellations we find in nature, functional design and art.
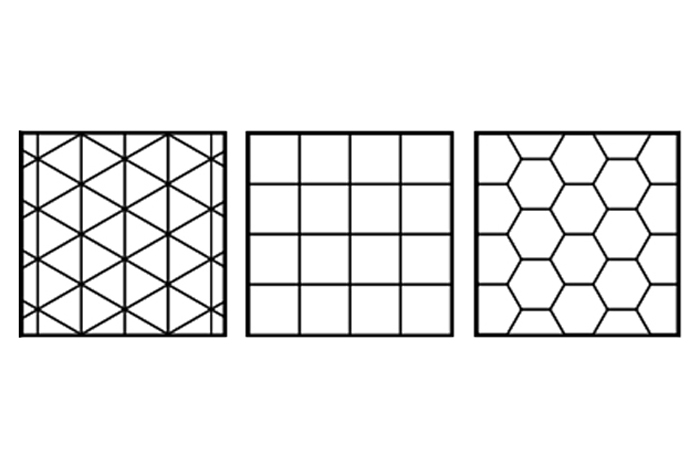
Regular tessellations
In mathematical terms, "regular" describes any shape that has all equal sides and equal angles. There are three regular shapes that make up regular tessellations: the equilateral triangle, the square and the regular hexagon. For example, a regular hexagon is used in the pattern of a honeycomb, the nesting structure of the honeybee.
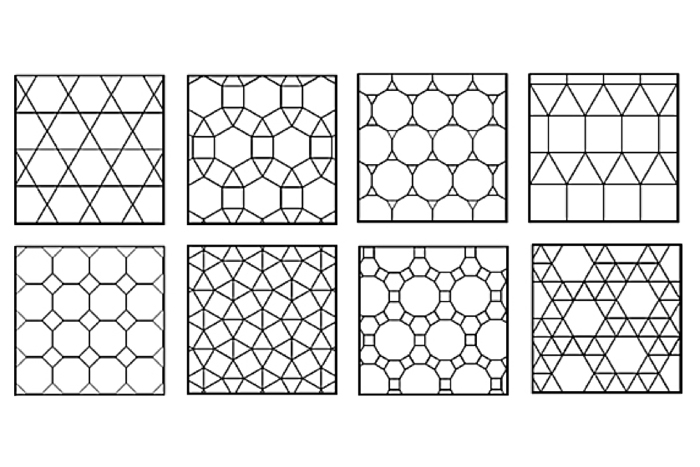
Semi-regular tessellations
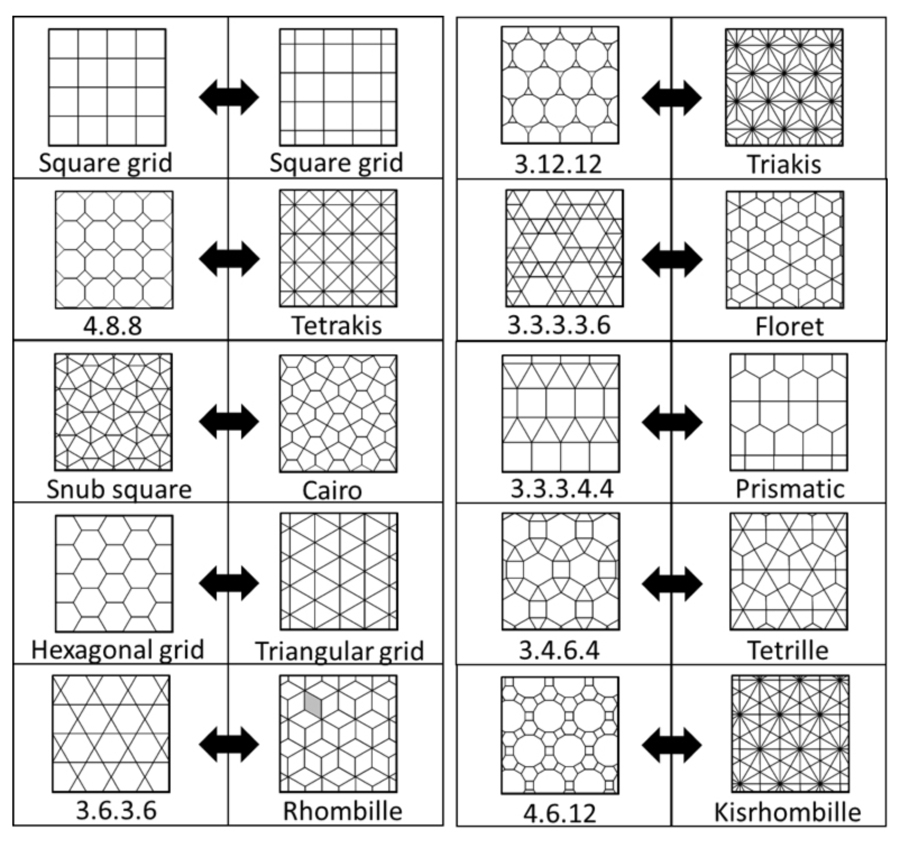
Semi-regular tessellations are made of more than one kind of regular polygon. Within the limit of the same shapes surrounding each vertex (the points where the corners meet), there are eight such tessellations. Each semi-regular tessellation is named for the number of sides of the shapes surrounding each vertex. For example, for the first tiling below, each vertex is composed of the point of a triangle (3 sides), a hexagon (6), another triangle (3) and another hexagon (6), so it is called 3.6.3.6. Sometimes these tessellations are described as "Archimedean" in honor of the third-century B.C. Greek mathematician.
Monohedral tessellations
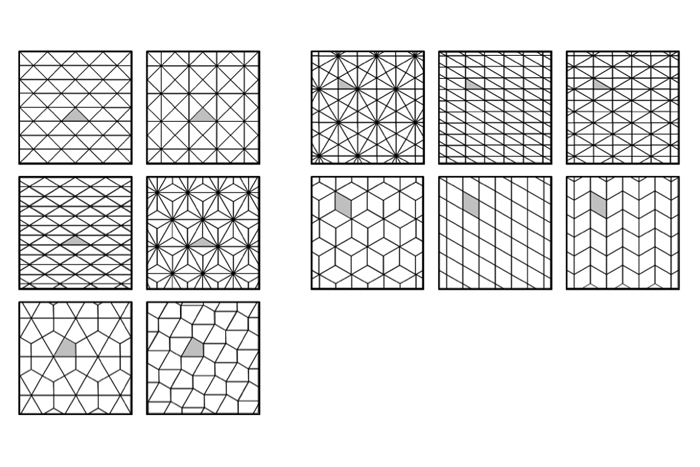
"Mono" means "one" and "-hedral" means "shape"; so monohedral tessellations are made up of only one shape, though the shape may be rotated or flipped. In the language of mathematics, the shapes in such a pattern are described as congruent. Every triangle (three-sided shape) and every quadrilateral (four-sided shape) is capable of tessellation in at least one way, though a select few can tessellate in more than one way. A few examples are shown below:
According to mathematician Eric W. Weisstein of Wolfram Research's MathWorld, for pentagons, there are currently 14 known classes of shapes that will tessellate, and only three for hexagons. Whether there are more classes remains an unsolved problem of mathematics. As for shapes with seven or more sides, no such polygons tessellate unless they have an angle greater than 180 degrees. Such a polygon is described as concave because it has an indentation.
A few examples of pentagonal tessellations are shown below. The 14 classes of pentagonal tessellation can all be generated at the Wolfram Demonstration Project.
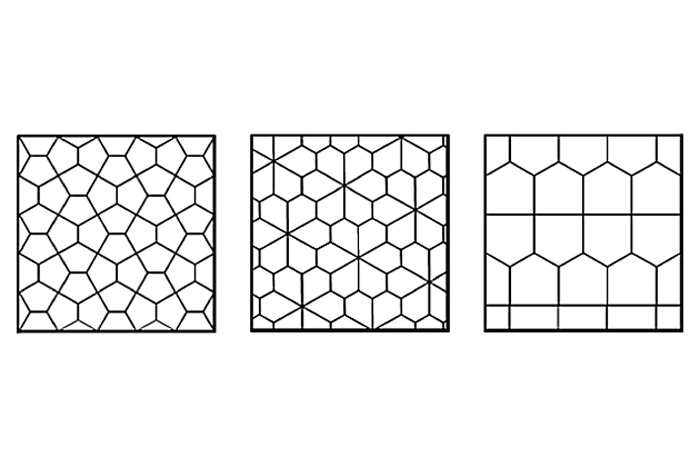
Duals
There's a deeper connection running through many of these geometric tessellations. A lot of them are "duals" of one another. According to Branko Grünbaum, author of "Tilings and Patterns" (Freeman, 1987), to create a tessellation's dual, draw a dot in the center of each shape, connect each dot to each of the neighboring shape's dots, and erase the original pattern. Below are some examples of tessellations and their duals:
M.C. Escher & modified monohedral tessellations
A unique art form is enabled by modifying monohedral tessellations. The most famous practitioner of this is 20th-century artist M.C. Escher. According to James Case, a book reviewer for the Society for Industrial and Applied Mathematics (SIAM), in 1937, Escher shared with his brother sketches from his fascination with 11th- and 12th-century Islamic artwork of the Iberian Peninsula. His brother directed him to a 1924 scientific paper by George Pólya that illustrated the 17 ways a pattern can be categorized by its various symmetries. This further inspired Escher, who began exploring deeply intricate interlocking tessellations of animals, people and plants.
According to Escher, "Crystallographers have … ascertained which and how many ways there are of dividing a plane in a regular manner. In doing so, they have opened the gate leading to an extensive domain, but they have not entered this domain themselves. By their very nature, they are more interested in the way the gate is opened than in the garden that lies behind it."
The following "gecko" tessellation, inspired by similar Escher designs, is based on a hexagonal grid. Notice how each gecko is touching six others.
Aperiodic tessellations
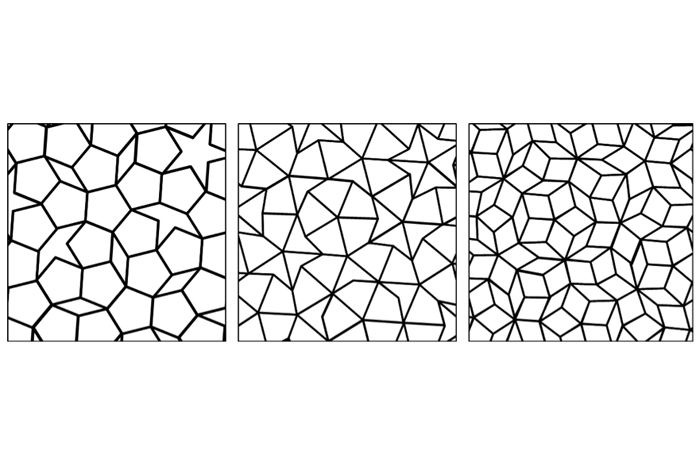
Not all tessellations repeat. Such a pattern (if it can be called that) is described as "aperiodic." Below are three versions of Penrose Tiling, named after English mathematical physicist Rodger Penrose, who first published such patterns in 1974 at the University of Oxford. These patterns exhibit five-fold symmetry, a property that is not found in any periodic (repeating) pattern.
Medieval Islamic architecture is particularly rich in aperiodic tessellation. The patterns were used in works of art and architecture at least 500 years before they were discovered in the West. An early example is Gunbad-i Qabud, an 1197 tomb tower in Maragha, Iran. According to ArchNet, an online architectural library, the exterior surfaces "are covered entirely with a brick pattern of interlacing pentagons."
The geometries within five-fold symmetrical aperiodic tessellations have become important to the field of crystallography, which since the 1980s has given rise to the study of quasicrystals. According to Peter J. Lu, a physicist at Harvard, metal quasicrystals have "unusually high thermal and electrical resistivities due to the aperiodicity" of their atomic arrangements.
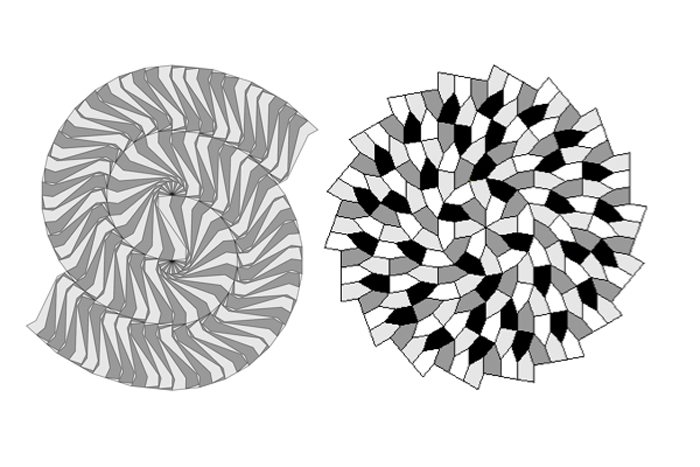
Another set of interesting aperiodic tessellations is spirals. The first such pattern was discovered by Heinz Voderberg in 1936 and used a concave 11-sided polygon (shown on the left). Another spiral tiling was published 1985 by Michael D. Hirschhorn and D.C. Hunt using an irregular pentagon (shown on the right).
Additional resources
- See M.C. Escher’s tessellations at the M.C. Escher Gallery.
- Watch this YouTube video to learn more about Penrose Tilings.
- Learn more about Peter J. Lu's ideas about the geometry of medieval Islamic architecture.
