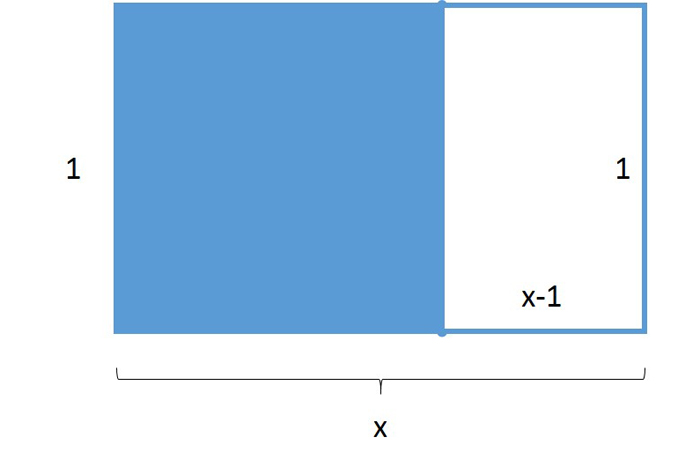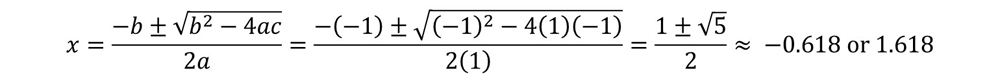What Are Quadratic Equations?

In mathematics, a quadratic is a type of problem that deals with a variable multiplied by itself — an operation known as squaring. This language derives from the area of a square being its side length multiplied by itself. The word "quadratic" comes from quadratum, the Latin word for square. 

Quadratic equations characterize a great number of phenomena in the real world, such as where a rocket ship will land, how much to charge for a product or how long it will take a person to row up and down a river. Because of their wide variety of applications, quadratics have profound historical importance and were foundational to the history of algebra.

The parabola

The math of quadratics is intrinsically related to a U-shaped curve known as a parabola. Perhaps the most familiar example is a stream of water that shoots from a drinking fountain. There are many other examples, such as the cross-section of a satellite dish or the cables on a suspension bridge.

The parabola was a significant shape to many mathematicians of ancient Greece, such as Euclid of Alexandria (~300 B.C.), Archimedes of Syracuse (287-212 B.C.), Apollonius of Perga (262-190 B.C.) and Pappus of Alexandria (A.D. 290-350). These scholars noted a number of mathematical properties intrinsic to parabolas:

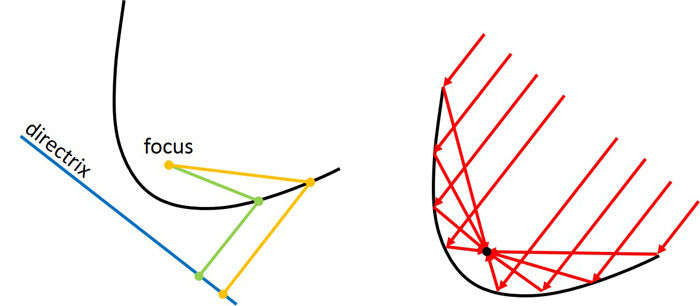
1. A parabola is the set of points equally distant from a point (a focus) and a line (a directrix). The appropriately named focus is important in a number of modern engineering applications, as it's the point on a parabolic dish to where incoming waves are reflected, be they radio waves (as in a satellite dish), light (as in a concentrating solar array) or sound (as in a parabolic microphone).

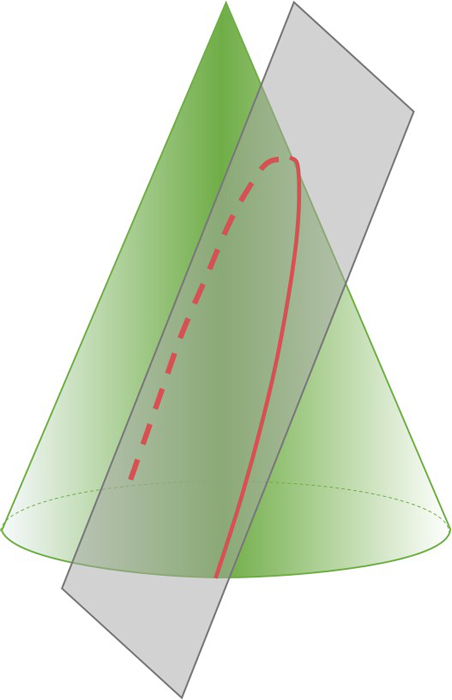
2. A parabola is also generated by cutting a cone parallel to the slope of the cone's sides. Because of this, parabolas are in a set of mathematical curves called conic sections. Nearly 2,000 years after this discovery, in his research on parabolic "burning mirrors," Leonardo da Vinci (A.D. 1452-1519) understood this property and developed a compass that could draw parabolas.

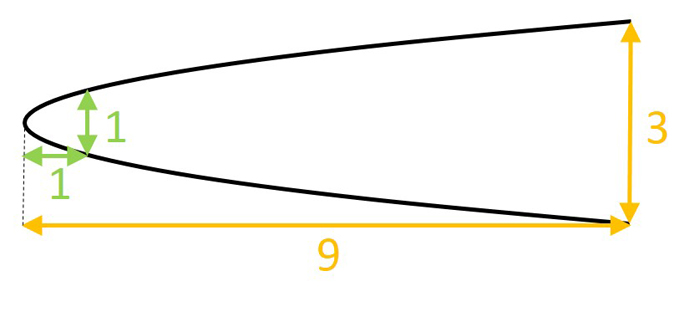
3. Changes in the height of a parabola are proportional to changes in the square of that parabola's width. For example, if a parabola is one unit high where it's one unit wide, it'll be nine (three squared) units high where it's three units wide. It's from this property that Apollonius derived the word "parabola" from parabole, the Greek word for "application," in the sense that the width is being "applied to" (multiplied by) itself. This is the property that links the shape of a parabola to the mathematical concept of the quadratic.

Though parabolas are ubiquitous, it is important to note that they're different from other U-shaped curves, such as a hanging chain (a catenary), the path of a child on a swing (a circular arc), the arc from an upright flashlight shining onto a wall (a hyperbola) or the crest of the side view of a spring (a sinusoid). These other curves don't have the previously mentioned properties of parabolas.

Projectile motion

The link between parabolas and the math of quadratics was of great significance in the 16th century A.D., when scholars of the European Renaissance noticed that projectiles such as cannonballs and mortars traveled in parabolic trajectories. Many notable scientists of that era, including Leonardo da Vinci and Galileo Galilei (1564-1642), studied projectile motion. According to Joseph W. Dauben, a professor of history at the City University of New York (CUNY), because artists of the Renaissance became obsessed with accurately portraying reality in art, Galileo became similarly obsessed with accurately portraying reality using mathematics. In 1638, Galileo published the first proof that a uniform acceleration from Earth's gravity would cause projectiles to move in parabolic trajectories. That mathematics could be used to describe motion was key to the progress of the Scientific Revolution.

Graphs of quadratics

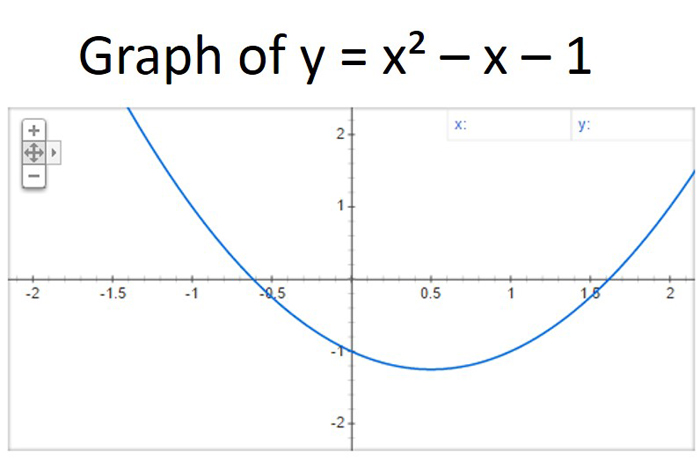
Around the same time as Galileo, French philosopher and mathematician René Descartes (1596-1650) published “La Géométrie” (1637), which described the technique of graphing algebraic equations in a field called analytical geometry. A variation of his methods is still used today. As shown below, the graph of a quadratic equation is a parabola.

An ancient quadratic: The golden ratio

To understand the quadratic-solving method that mathematicians, scientists and engineers use today, let's explore an ancient math problem: the golden ratio. As an aside, in "Misconceptions about the Golden Ratio" (1992), George Markowsky, a math professor at the University of Maine, pointed out that the golden ratio's historical significance and aesthetic appeal are often overstated, though it is true the ratio appears often in number theory (in parallel with the& Fibonacci sequence), geometry (such as in an icosahedron) and biology (such as the angle between a plant's leaves). 

One method of determining the golden ratio is stated thusly:

Find rectangle with a length and width such that when a square is cut off one end of the rectangle, the remaining scrap rectangle will have the same shape or "aspect ratio" as the original rectangle (but rotated at a right angle).

While the ancient Greeks solved this problem using geometry, we'll use algebra as it is taught today.

To determine what length and width will produce the golden ratio, we give the short side a length of 1 and the long side a length of x. Because aspect ratio is defined as the long side divided by the short side, the aspect ratio for this rectangle is x/1, or simply x. If we cut a square off of this rectangle, the remaining scrap has a long-side length of 1 and a short-side length of x – 1. Thus, the aspect ratio is 1/(x – 1). Understanding that the aspect ratio for the overall rectangle and the smaller scrap rectangle should be the same, our equation is x = 1/(x – 1).

The quadratic formula

Here's how students are instructed to solve this equation today. Start with the equation:

x = 1/(x – 1)

Multiply each side of the equation by the expression x – 1:

x·(x – 1) = 1

Distribute the x across the expression x – 1:

x·x – x·1 = 1

The variable x multiplied by itself is written as x². This squaring is what makes the equation a quadratic:

x² – x = 1

Now, we subtract 1 from each side of the equation to achieve what is known as the standard form of a quadratic equation:

x² – x – 1 = 0

Equivalently, this may be written as:

(1)·x² + (-1)·x + (-1) = 0

When this is compared to the equation a·x² + b·x + c = 0, it gives values of a = 1, b = -1 and c = -1. These values are used in the quadratic formula as

The symbol "±" means "plus or minus." Because of this, the quadratic formula always gives two solutions. Substitute either of these values into the equation x = 1/(x – 1) to test whether this makes both sides of the equation come out the same. It does, meaning the method worked. Notice these values are also the places at which the graph of the standard form of the equation (y = x² – x – 1) crosses the X axis, which is where y = 0 (see graph above). In this case, the positive value is of greater physical significance, because a rectangle shouldn't have negative width.

Ancient Babylonian origins

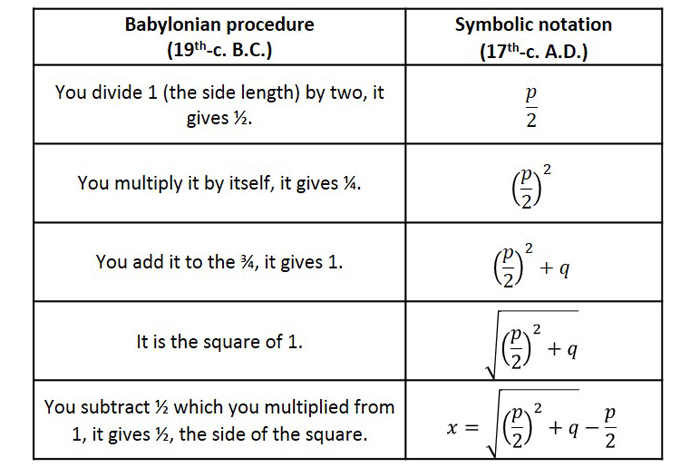
To offer some insight into where the quadratic formula comes from and why it works, let us examine a procedure used on an ancient Babylonian clay tablet from around 1800 B.C. (Tablet BM 13901, British Museum). According to Jacques Sesiano in "An Introduction to the History of Algebra" (AMS, 2009) the first problem on this tablet translates approximately to:

I added the area and the side of a square to get ¾. What is the side of the square?

The problem is written in modern notation as:

x² + x = ¾

The following is a retelling of the Babylonian and Arabic methods as described by Sesiano. First, we'll translate the steps the Babylonians used, but also translate them to symbolic language we use today in algebra. Fully symbolic language first appeared in Europe in the 17 century. Because the Babylonians didn't know about negative numbers, it is necessary to write the equation in the form x² + px = q, where p = 1 and q = ¾. When comparing this to the modern standard form ax²& + bx + c = 0, it shows that p = b/a and q = -c/a.

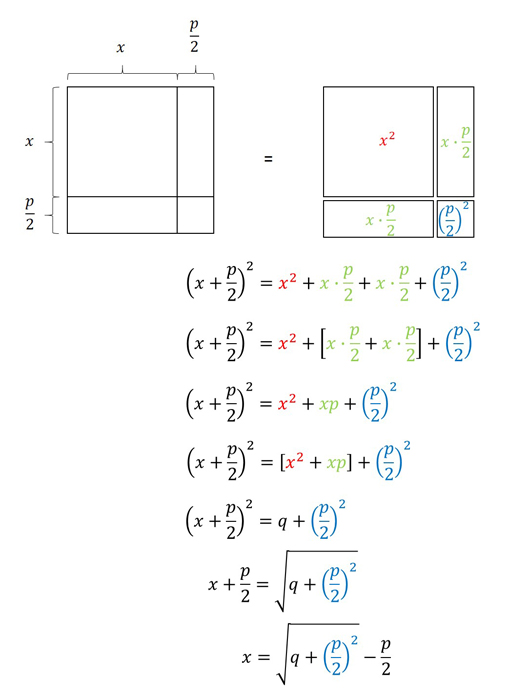
Now let's derive and prove the procedure is correct using geometric methods as Arabic mathematicians did in the ninth-century A.D. The following is a variation of a proof that appeared in Persian mathematician Al-Khwārizmī's publication of "The Compendious Book on Calculation by Completion and Balancing" in A.D. 820. Although the Babylonians almost certainly derived their procedural methods from geometry, neither written records of derivation nor proofs of correctness appeared until the Golden Age of Islam, a period from the mid-seventh century to the mid-13th century, when Muslims ruled an empire that stretched from Central Asia to North Africa and Iberia.

If we "plug in" p = b/a and q = -c/a, the formula indeed simplifies to the modern form of the quadratic equation as it is taught today.

Various forms of the quadratic formula were used across Afro-Eurasia over the ages. Procedural versions were used by the Babylonians and Egyptians around the 19th century B.C., the Chaldeans in the seventh century B.C., the Greeks in the fourth century B.C. and the Indians in the fifth century A.D. Rhetorical and syncopated forms were developed by the Arabs in the ninth century A.D., and syncopated and symbolic forms by the Europeans in the 11th century A.D. The methods used by each civilization progressed as more was learned about negative, irrational, imaginary and complex numbers.

Additional resources

• Drexel University has an entertaining Web page that illustrates the history of graphing.
• Purplemath.com, a math lessons site, explains conics and parabolas.
• MathWorld, an online math resource, discusses quadratic equations.