Topology is a branch of mathematics that describes mathematical spaces, in particular the properties that stem from a space’s shape. Many of the shapes topologists deal with are incredibly strange, so much so that practically all everyday objects such as bowls and pets and trees make up a small minority. The word “topology” derives from the Greek words for place (topos) and study (-logy).
Topology is important as a guide in several areas of study:
- Theoretical physics (in particular the successors of quantum mechanics such as quantum field theory and string theory)
- Cosmology (for determining the shape of the universe)
- Biology (for the tangling of DNA and predicting the growth of organs and other body parts)
- Computer science (for determining the large-scale structure of data sets)
- Robotics (where a robot arm’s motions are planned based on the shape of a space with a number of dimensions equal to the number of arm joints)
Continuous deformation
A topologist studies properties of shapes, in particular ones that are preserved after a shape is twisted, stretched or deformed. This list of allowed changes all fit under a mathematical idea known as continuous deformation, which roughly means “stretching, but not tearing or merging.” For example, a circle may be pulled and stretched into an ellipse or something complex like the outline of a hand print. Tearing and merging cause what are known as discontinuities, so they’re not allowed.
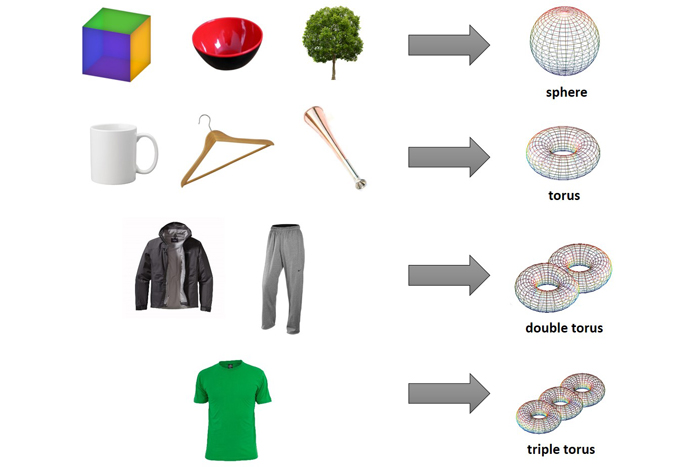
Two objects that can be stretched into the same shape are described as homeomorphic, from Latinized Greek for “similar to” (homeo-) and Greek “form, shape, or figure” (morphe). Through this lens, virtually all everyday objects are homeomorphic with a sphere (a ball) or some variety of torus (a donut).
Some branches of topology allow an object to pass through itself while being stretched; others do not. When considering a surface that can pass through itself, it’s important not to pinch a surface infinitely tight, since this also adds discontinuities. This is usually encountered when a surface is doubled back on itself, such as when trying to turn a sphere inside out (which is difficult, but possible).
Euler Characteristic
One example of a property that is doesn’t change under continuous deformation is an object’s Euler characteristic, named after Leonhard Euler, an 18th-century German mathematician.
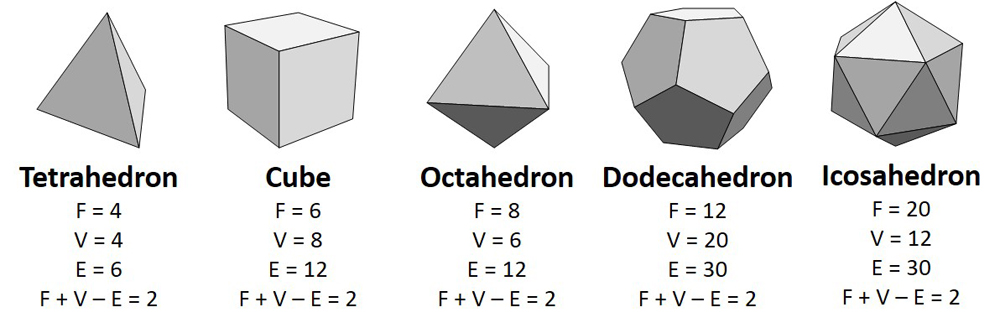
To demonstrate an object’s Euler characteristic, first we take a sphere (or an object homeomorphic with a sphere, like a human head) and tile the surface with polygons. Then, we count the number of faces (sides), edges (places where two sides meet), and vertices (places where three or more sides meet). Now, add the number of faces (F) and vertices (V) and subtract the number of edges (E): F + V – E. It doesn’t matter how you divide up the surface; the answer will always come out the same: two. Since the five platonic solids (the 3-D shapes made from one kind of regular polygon) are all homomorphic to a sphere, they also all have an Euler characteristic of two.
We can make sense why the Euler characteristic is conserved if we think about what it means to add an edge or vertex. Adding an edge between two vertices splits one face into two: Edges increase one, faces increase one, and vertices stay the same. Likewise, adding a vertex along an edge splits the edge into two: Edges increase one, vertexes increase one, and faces stay the same.
Now tile the surface of a torus, count F, V, and E, and you’ll get an Euler characteristic of zero. Here’s an example:
With a double torus, the Euler characteristic is negative two; for a triple torus, negative four. Each additional hole reduces the Euler characteristic by two.
Non-orientable surfaces
One thing all the shapes we’ve talked about thus far have in common is they’re said to be orientable. This means a bug walking on the outside surface will always remain on the outside; the same goes for the inside. There are also non-orientable surfaces, meaning a bug wandering on the surface can end up on both sides. The most famous example of this is the Mobius strip (which has an Euler characteristic of zero, EC = 0).
While language like “both sides of a Mobius strip” is useful for introducing the concept, it runs counter to the mind of a topologist, who says any surface is 2-D, and so are the beings that inhabit it. Through this lens, it’s more useful to think of a 2-D bug living within the surface itself. For an orientable surface, there are right-handed bugs and left-handed bugs, but for a non-orientable surface, right- and left-handed bugs are indistinguishable. This emphasizes that the Mobius strip represents a space and that we are interested in the properties that stem from the space’s shape.
Fundamental polygons
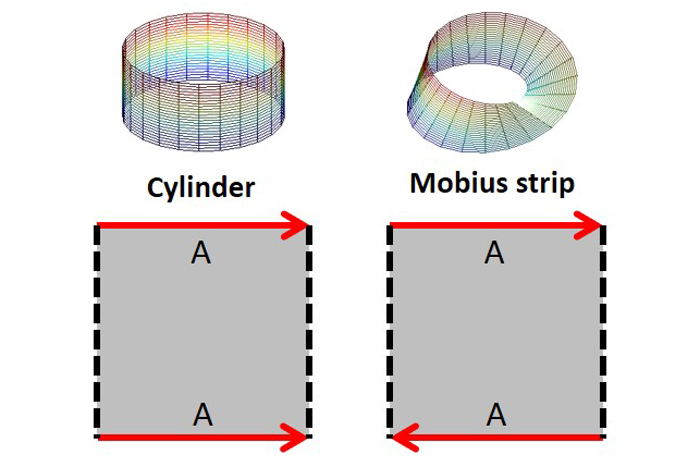
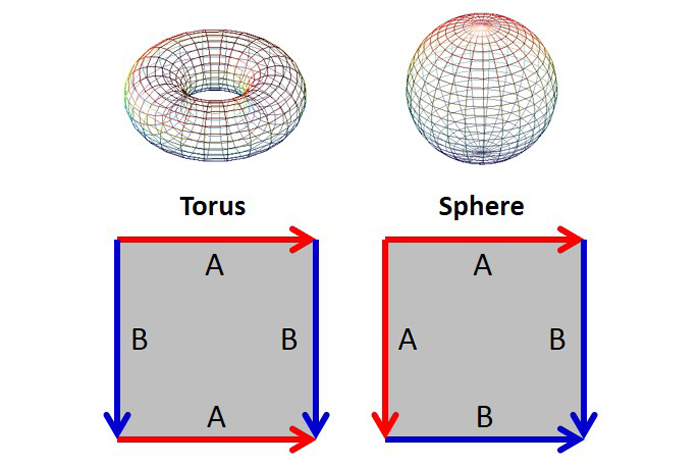
With this perspective of surfaces being 2-D, it is convenient to represent the topological spaces in terms of their fundamental polygons. To turn the 2-D surface of a fundamental polygon into a 3-D object, stretch the surface so the corresponding sides join in the direction indicated by the arrows. As can be seen, joining parallel sides makes a cylinder (EC = 0), and joining anti-parallel lines makes a Mobius strip (EC = 0).
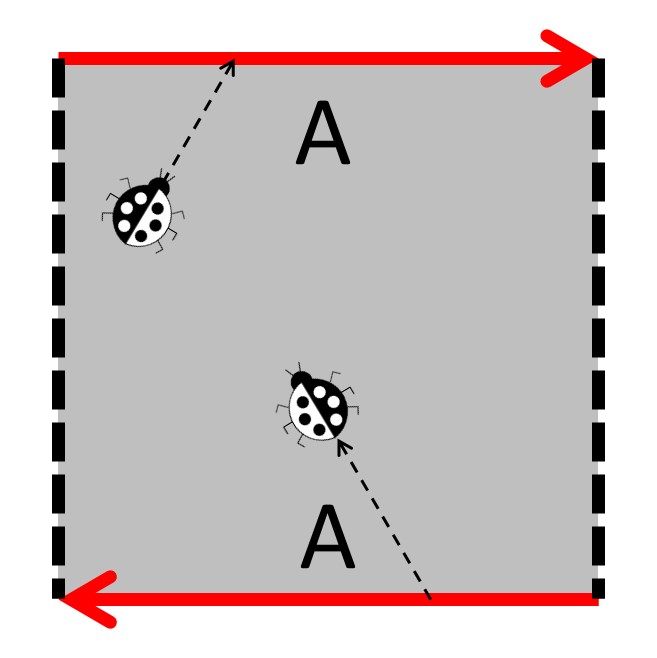
A 2-D bug that walks off and arrowed boundary of a fundamental polygon is transported to the other boundary, and oriented in the same way compared to the direction of the arrow. Whether the bug stays the same or flips indicates if the surface is orientable or non-orientable, respectively. A 2-D bug is not allowed to cross a dotted boundary.
The first shapes we talked about also have fundamental polygons. To make a torus, first make a cylinder, then stretch the ends of the cylinder until they meet. To make a sphere, fold the sheet from corner to corner to make a triangular envelope, then inflate it until it’s spherical.
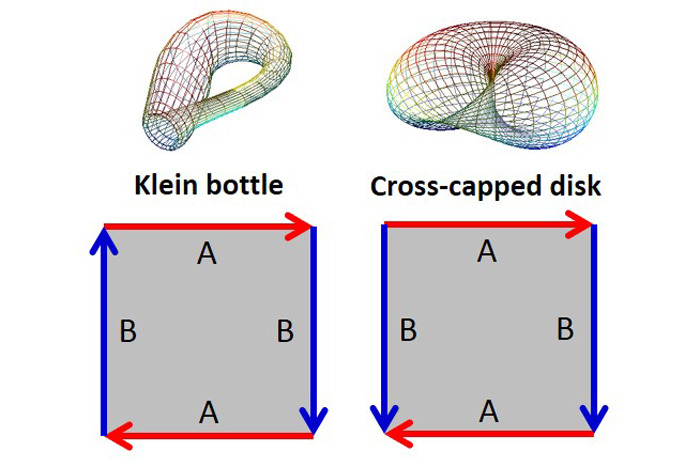
The dotted edges of a Mobius strip can be combined in two different ways to give rise to two more non-orientable surfaces: a Klein Bottle (EC = 0) can be thought of as a cross between a Mobius strip and a cylinder, and a cross-capped disk (EC = 1) can be thought of as the cross between two Mobius strips. As with the Mobius strip, if there is a third dimension to wrap this map in, we can gain some perspective of the overall “shape” of the space. Both constructions require that the surface be allowed to pass through itself. A 2-D bug would not notice such an intersection; only that the world is “flipped” after taking certain paths in the 2-D space.
Famous problems in topology
Topology has existed for only a few centuries, but already has a rich history of problems and subfields that each has a story of its own.
- Seven Bridges of Königsberg: Often considered the first problem in topology. The Old Prussian town of Königsberg once had seven bridges, and its people wondered if it was possible to walk a path that only crossed each bridge once. In 1735, Euler proved that such a path was impossible.
- Patterns in Palm and Finger Prints: Fingerprints all have common features such as loops and triradii (three lines coming together). In 1965 Lionel Penrose, a British medical geneticist, pointed out that fingerprints and palm prints obey a universal rule: everybody born with five fingers always has four more triradii than loops.
- Hairy Ball Theorem: For a ball (or sphere, rather) covered in hair, it is impossible to comb all the hair flat. There must be at least one place where the hair sticks straight up.
- Sphere Eversion: For a spherical surface that’s allowed to pass through itself, is it possible to turn a sphere completely inside-out without pinching any region infinitely tight? It’s tricky, but yes.
- Knot Theory: Knot theory is a discipline within topology that only deals with tori (plural of torus) that cannot pass through themselves or others. A major focus of knot theory is to determine whether two different-looking knots are homeomorphic.
- Poincaré Conjecture: In this article, we have only examined 2-D spaces, but there are also 3-D spaces that connect in strange ways. The Poincaré Conjecture, first posed in 1904, is about these 3-D spaces, stating that “every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.” Nearly a century later, in 2000, the Clay Mathematics Institute selected seven unsolved “Millennium Prize” problems for which $1 million would be awarded to anyone finding a solution. The Poincaré Conjecture was the first such problem to be solved. Russian mathematician Grigori Perelman, who found the solution in 2002, declined both the Millennium cash prize and the Fields Medal (considered by many to be the equivalent of a Nobel Prize in Mathematics).
Additional resources
