'The beauty of symbolic equations is that it's much easier to … see a problem at a glance': How we moved from words and pictures to thinking symbolically

For many, the idea of math will bring back endless hours of formulas and equations at school. So it may seem hard to imagine, but there once was a time when arithmetic didn't exist. Of course, there was still the need to use complex computations to solve real-world problems, but it wasn't until Muhammad ibn-­Mūsā al-­Khwārizmī, the so-called "father of algebra," established the fundamentals for solving equations that we began to set the foundations for modern mathematics.

In this excerpt from her new book "Vector: A Surprising Story of Space, Time, and Mathematical Transformation", mathematician Robyn Arianrhod explores the 4,000-year evolution of the language of mathematics — from complex descriptions to the symbolic form we know today.

Learning to think symbolically

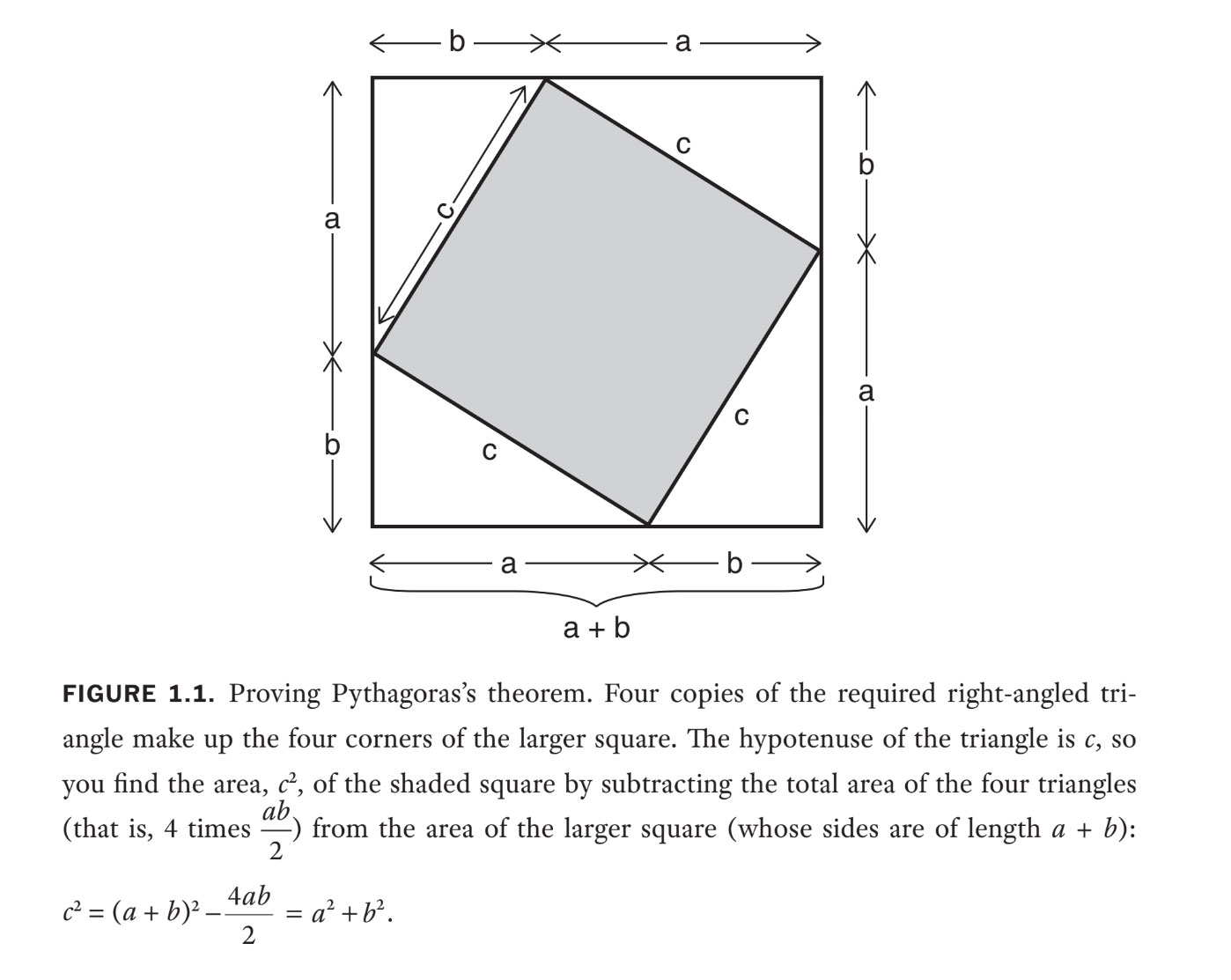
Algebra has been part of mathematics since records began nearly 4,000 years ago, but not always in the symbolic form we learn today. In fact, for most of those four millennia it was written entirely in words and numerals — although works such as Euclid’s famous 300 B.C.E. textbook "Elements" also included geometric diagrams, to help prove such things as Pythagoras's theorem, and to show how to expand squares that we would write today as (a+b)².

Latest Videos From

Watch full video here:

So "algebra" was communicated in cumbersome word problems or increasingly complicated diagrams — although geometry did have its advantages. For instance, it's the easiest way to prove Pythagoras's theorem. In figure 1.1, I've given an algebraic adaptation of such a proof, although the ancients simply rearranged the diagram to show visually that the shaded area is equal to the sum of the areas of the squares on the adjacent sides of the triangle — a pretty clever approach!

It took a long time for algebra to emerge from arithmetic and geometry as a separate subject. It didn't even get its name until medieval times, and that was thanks to the ninth-­century Persian mathematician Muhammed ibn-­Mūsā (al-­)Khwārizmī… He studied at Caliph al-­Ma’mūn’s pioneering Baghdad-­based university, or "House of Wisdom," when the great Arabic translation movement was at its height: Greek, Indian, and other ancient manuscripts were being collected from all corners of the burgeoning Islamic empire and translated into Arabic.

Imperialism is rarely ethical and often violent, but it can ultimately lead to cultural cross-­fertilization, and in this case the visionary translation movement was so important that by the 12th century, Europeans were learning Arabic in order to translate these manuscripts into Latin — including Ptolemy’s "Almagest" and Euclid’s "Elements," along with new Arabic works such as those of al-­Khwārizmī. The name "algebra” famously comes from the first word in the title of his book "Al-Jabr wa’l muqābalah" — which means something like "The Compendious Book on Calculation by Completion and Balancing."

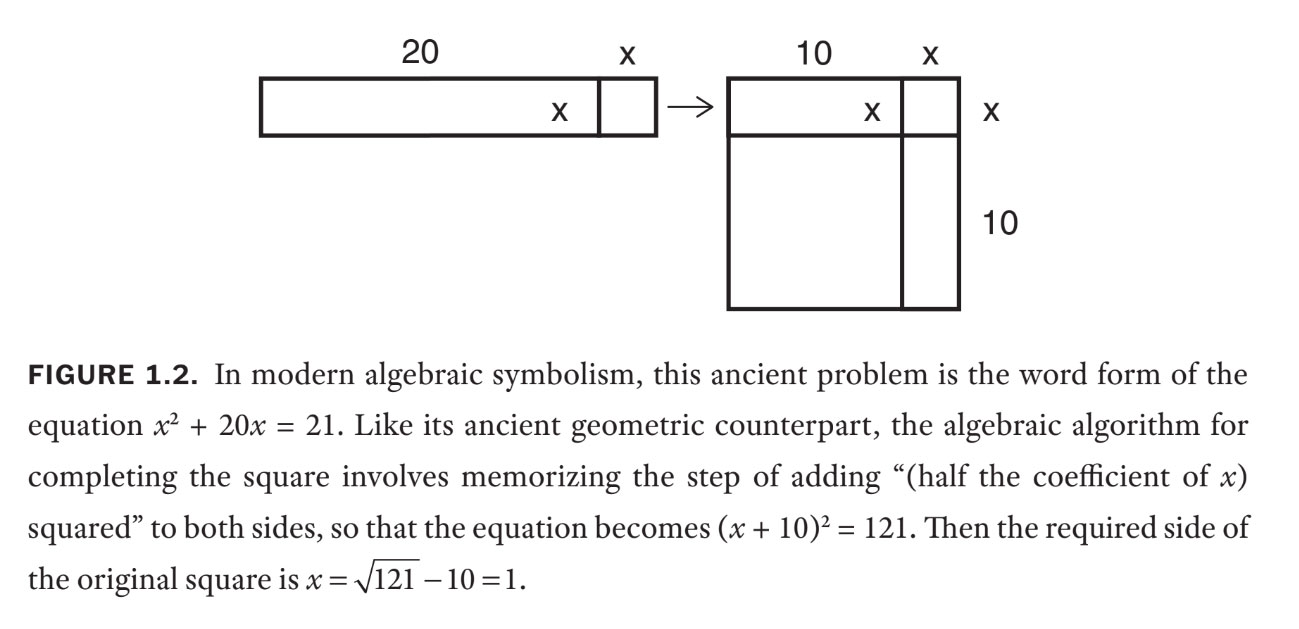
Judging from the problems al-­Khwārizmī included, an example of what he meant by "Completion" is "completing the square," the method you might have learned in school to solve quadratic equations...

Al-­Khwārizmī didn't write equations in the symbolic form we use today, either. In fact, to modern eyes his book is more arithmetical than algebraic, and one of its important impacts in Europe, when it was translated into Latin, was the popularization of the Hindu-­Arabic decimal system of numeration that eventually evolved into our modern one.

Yet Al-­Khwārizmī is often called the "father of algebra." He may have used words rather than symbols, and the problems he included may have been simple — his purpose, he tells us, was to teach students how to solve basic problems in "cases of inheritance, legacies, partitions, lawsuits and trade, and in all their dealings with one another, or where the measuring of lands, the digging of canals, geometrical computation, and other objects of various sorts and kinds are concerned."

But he systematically set out word-­form linear and quadratic equations, with algorithmic methods for solving them — that is, for finding the "unknown numbers," our modern x's and y's. In fact, the English word "algorithm” — meaning a set of rules for performing a calculation or other operation — comes from "algorismi,” an early Latinized attempt at Al-­Khwārizmī.

…

The beauty of symbolic equations is that it's much easier to see these general patterns when you can see a problem at a glance. Compare this:

Take the square of the unknown number,

then add the unknown number to itself

and take the sum away from the square;

now let the total be eight.

with this:

x²–2x=8

And there's more: The earliest mathematicians solved each equation separately, but it's easier if you can see that whatever method works for the equation x²–2x=8 will also work for any equation of the same form, x²–ax=b. Eventually, ancient mathematicians did begin to recognize this, but progress was relatively slow because they had to keep all these patterns in their heads, or in long, convoluted sentences, and it was easy to lose track.

The first to publish any equation in a transparent, recognizably modern symbolic form were [Thomas] Harriot's executors in 1631, and then [René] Descartes in an appendix to his 1637 "Discourse on Method." (There were a few earlier attempts, but the symbolism — more properly called abbreviation — was tortured and idiosyncratic.) Even the +, −, =, and × signs we take for granted only came into widespread use in the 17th century. Which means that the earlier algebraists we know of — the ancient Mesopotamians, Egyptians, Chinese, and Greeks, the medieval Indians, Persians, and Arabs, as well as the early modern Europeans — all had expressed their equations mostly in words or pictorial word images.

Related: 9 equations that changed the world

It is a singular skill to think symbolically, as this long history shows. Take the word problem I gave above: it is an example of algorithmic thinking. But symbolic thinking is algorithmic and more, for its symbols sometimes contain the seeds of a new kind of creativity — a new kind of far-­reaching yet economical thought.

A classic case is Albert Einstein’s E=mc². Einstein did not set out to find the connection between energy and matter. Rather, he simply wanted to calculate the kinetic energy of a moving electron according to his new theory of relativity, so that his theoretical prediction could be tested experimentally.

A few months later, however, 26-­year-­old Einstein began to realize the significance of his equation. He wrote it up in his fifth groundbreaking paper of 1905, his annus mirabilis, but it would take him two more years to tease out the full, dramatic implications of this symbolic relationship. To realize that this wasn’t just a calculation about a particular form of energy and a particular type of matter, it was general: if a body gains (or loses) energy, it also gains (or loses) mass. This bizarre idea is alien to all our commonsense experience — but there it was, hidden in the symbols of his equation. It took experimental physicists decades to experimentally confirm this astonishing mathematical prediction.

A much simpler and earlier example is the sequence of powers x, x², x³ and so on. The first "power" is 1, so x is really x¹ , where the 1 was traditionally linked geometrically to a 1-­D line. The next two, x² and x³, are pronounced "x squared" and "x cubed" by analogy with the area of a square and the volume of a cube. These names highlight the way that early mathematicians thought geometrically rather than algebraically, because of the tangible nature of geometry. By contrast, symbolic algebra is abstract: you have to give it meaning, even if it is simply the display of an interesting pattern such as x, x², x³, x⁴,... But this flexibility is algebra's great strength. You can write down as many (finite) higher powers as you like, without having to visualize them as physical objects.

This may sound obvious today, but it took three and a half thousand years for mathematicians to move from solving quadratic equations — "quadratic" derives from the Latin for "square," so quadratic equations are those whose highest power is x² (the unknown multiplied by itself, as the ancients put it) — to solving "cubic" and higher equations. These higher-degree equations are much more difficult, of course; but part of the reason solutions didn't come easily was that algebra was tied to words and concrete images for such a very long time.

For instance, I mentioned Al-­Khwārizmī’s "completing the square" in order to solve a quadratic equation. It's actually a 4,000-­year-­old problem, dating back (as far as the historical record shows) to cuneiform tablets made by mathematicians living, like Al-Khwārizmī, in the region of modern-­day Iraq. These ancient Mesopotamians solved quadratic equations by literally completing a square.

Here is a typical teaching problem of the time: "Add 20 of my length to the area of my square, [to get] 21. How square is my square?" This type of problem, and the algorithm for solving it, is similar to those taught today — except that four millennia ago, the method was worked out entirely geometrically. First, draw a square of arbitrary side x (in modern notation); then add to it a rectangle of dimensions 20 [by] x. Now split this additional rectangle into two equal smaller ones and arrange them beside and below the original square. Finally, complete this new, larger square, as in figure 1.2.

The Mesopotamians had practical problems in mind when they developed this method, at least initially. Living in a land where water was at a premium, their tablets contain many problems relating to canal and reservoir excavations, the capacity of cisterns, the construction and repair of dams and levees, and administrative accounts relating to these tasks — and to solve these problems, these ancient mathematicians had to solve equations relating to areas and volumes.

Nearly 3,000 years later, Al-­Khwārizmī, too, focused on similar practical problems, and he used a similar geometrical method of completing the square — and so did other mathematicians right up to the 17th century.

Vector: A Surprising Story of Space, Time, and Mathematical Transformation by Robyn Arianrhod is available now — $22.71 on Amazon

Algebra is just one of the many ways we make sense of the mathematical world, and if this excerpt piques your interest, why not delve deeper into the book and discover how something seemingly so simple as a vector changed the way we shape space and even time.