Mathematical equations offer unique windows into the world. They make sense of reality and help us see things that haven't been previously noticed. So it’s no surprise that new developments in math have often gone hand in hand with advancements in our understanding of the universe. Here, we take a look at nine equations from history that have revolutionized how we look at everything from tiny particles to the vast cosmos.
Pythagorean theorem
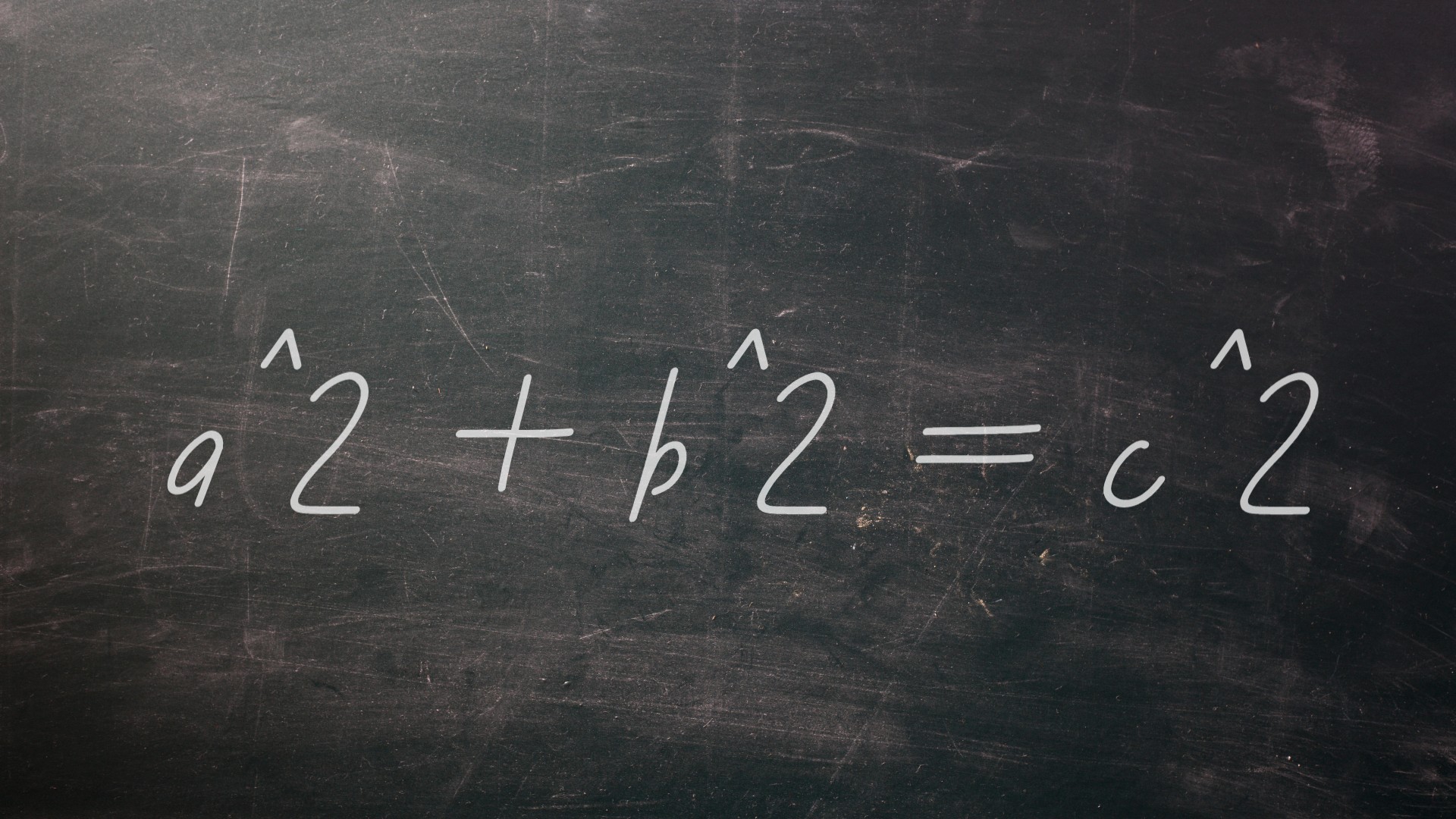
One of the first major trigonometric rules that people learn in school is the relationship between the sides of a right triangle: the length of each of the two shorter sides squared and added together equals the length of the longest side squared. This is usually written as a^2 + b^2 = c^2, and it has been known for at least 3,700 years, since the time of the ancient Babylonians.
The Greek mathematician Pythagoras is credited with writing down the version of the equation used today, according to the University of St. Andrews in Scotland. Along with finding use in construction, navigation, mapmaking and other important processes, the Pythagorean theorem helped expand the very concept of numbers. In the fifth century B.C., the mathematician Hippasus of Metapontum noticed that an isosceles right triangle whose two base sides are 1 unit in length will have a hypotenuse that is the square root of 2, which is an irrational number. (Until that point, no one in recorded history had come across such numbers.) For his discovery, Hippasus is said to have been cast into the sea, because the followers of Pythagoras (including Hippasus) were so disturbed by the possibility of numbers that went on forever after a decimal point without repeating, according to an article from the University of Cambridge.
F = ma and the law of gravity
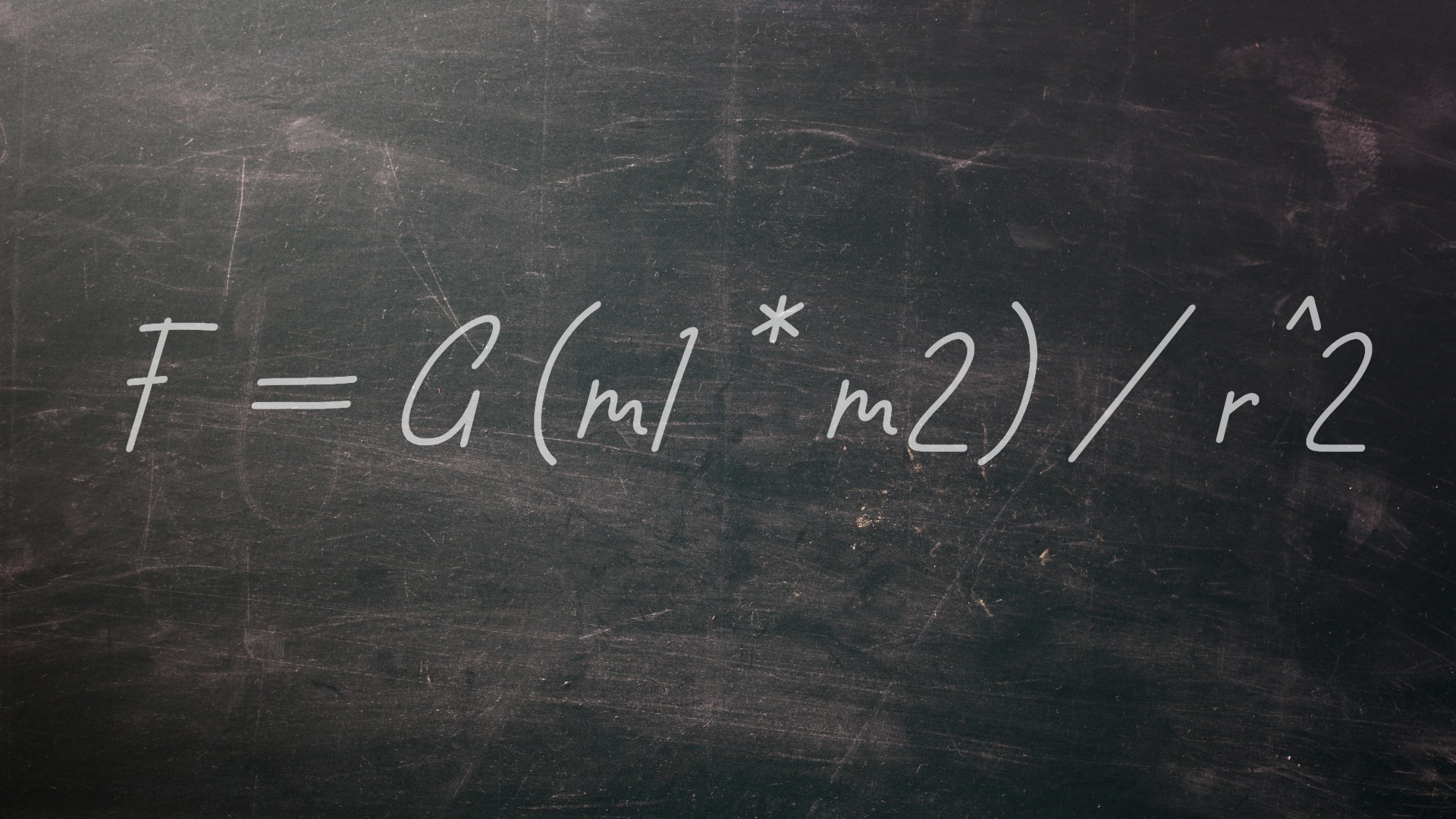
British luminary Sir Isaac Newton is credited with a large number of world-shattering findings. Among them is his second law of motion, which states that force is equal to the mass of an object times its acceleration, usually written as F = ma. An extension of this law, combined with Newton's other observations, led him, in 1687, to describe what is now called his law of universal gravitation. It is usually written as F = G (m1 * m2) / r^2, where m1 and m2 are the masses of two objects and r is the distance between them. G is a fundamental constant whose value has to be discovered through experimentation. These concepts have been used to understand many physical systems since, including the motion of planets in the solar system and the means to travel between them using rockets.
The wave equation
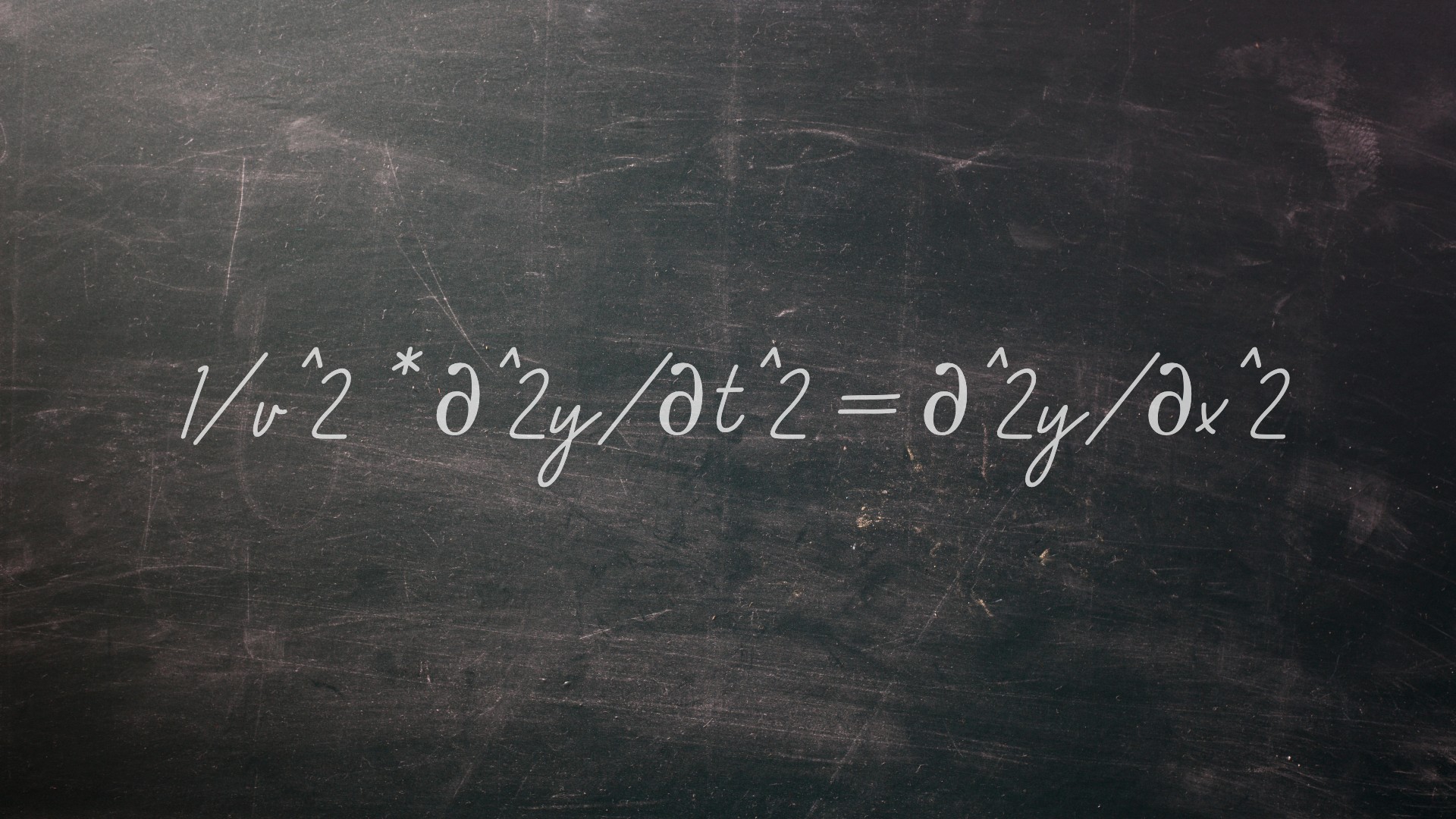
Using Newton's relatively new laws, 18th-century scientists began analyzing everything around them. In 1743, French polymath Jean-Baptiste le Rond d'Alembert derived an equation describing the vibrations of an oscillating string or the movement of a wave, according to a paper published in 2020 in the journal Advances in Historical Studies. The equation can be written as follows:
1/v^2 * ∂^2y/∂t^2= ∂^2y/∂x^2
In this equation, v is the velocity of a wave, and the other parts describe the displacement of the wave in one direction. Extended to two or more dimensions, the wave equation allows researchers to predict the movement of water, seismic and sound waves and is the basis for things like the Schrödinger equation of quantum physics, which underpins many modern computer-based gadgets.
Fourier’s equations
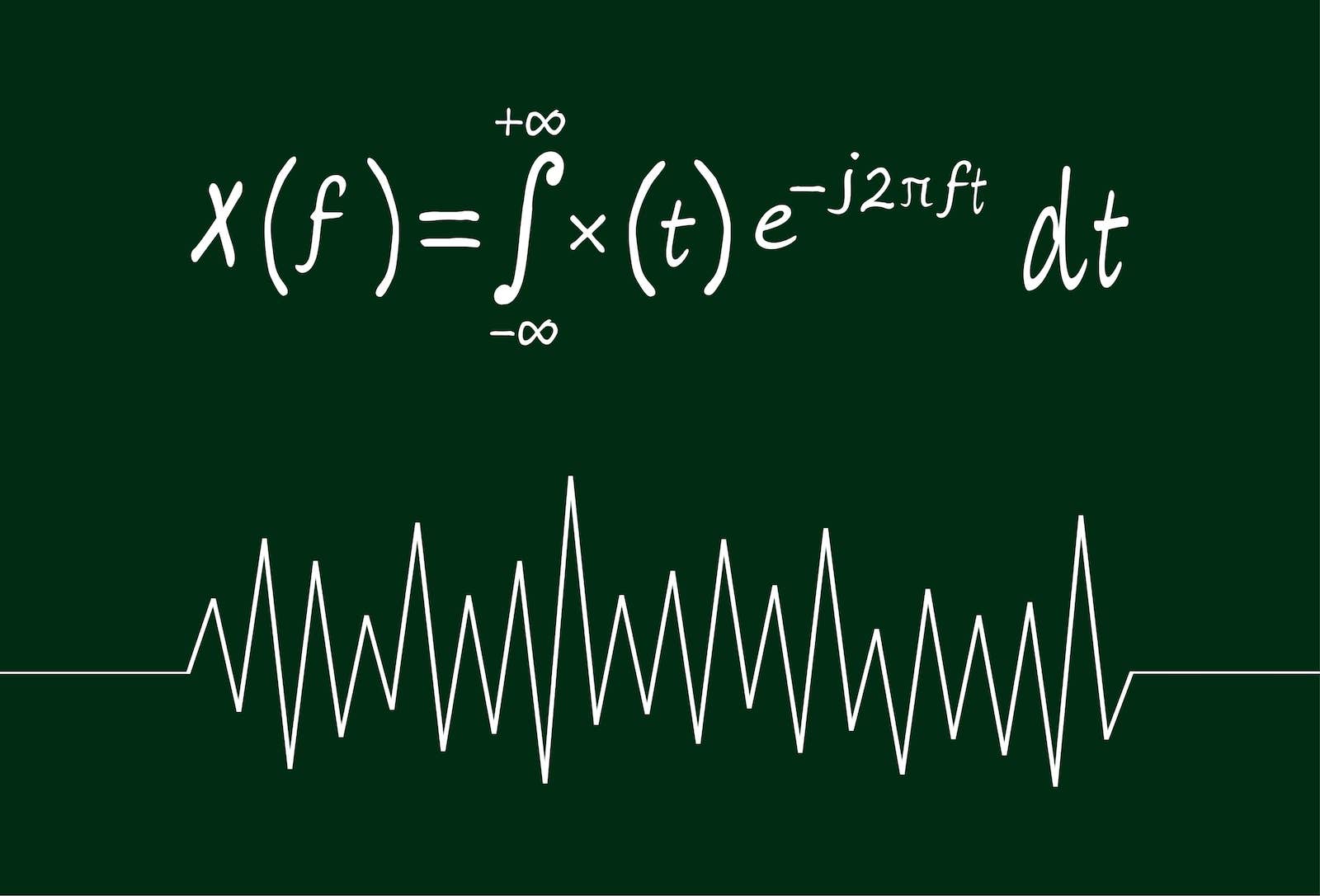
Even if you haven't heard of the French baron Jean-Baptiste Joseph Fourier, his work has affected your life. That's because the mathematical equations he wrote down in 1822 have allowed researchers to break down complex and messy data into combinations of simple waves that are much easier to analyze. The Fourier transform, as it's known, was a radical notion in its time, with many scientists refusing to believe that intricate systems could be reduced to such elegant simplicity, according to an article in Yale Scientific. But Fourier transforms are the workhorses in many modern fields of science, including data processing, image analysis, optics, communication, astronomy and engineering.
Maxwell's equations
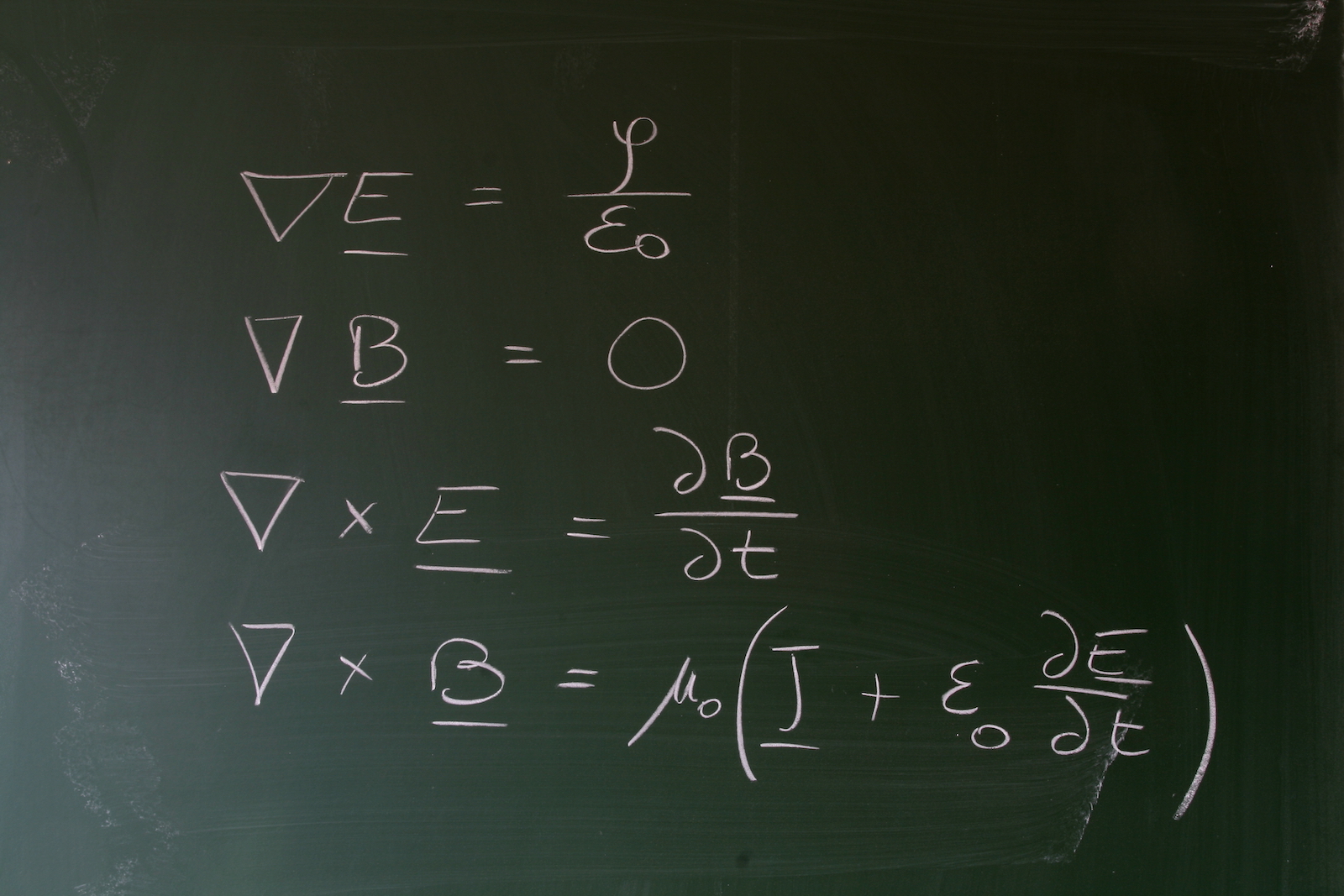
Electricity and magnetism were still new concepts in the 1800s, when scholars investigated how to capture and harness these strange forces. Scottish scientist James Clerk Maxwell greatly boosted our understanding of both phenomena in 1864, when he published a list of 20 equations describing how electricity and magnetism functioned and were interrelated. Later honed to four, Maxwell's equations are now taught to first-year physics students in college and provide a basis for everything electronic in our modern technological world.
E = mc^2
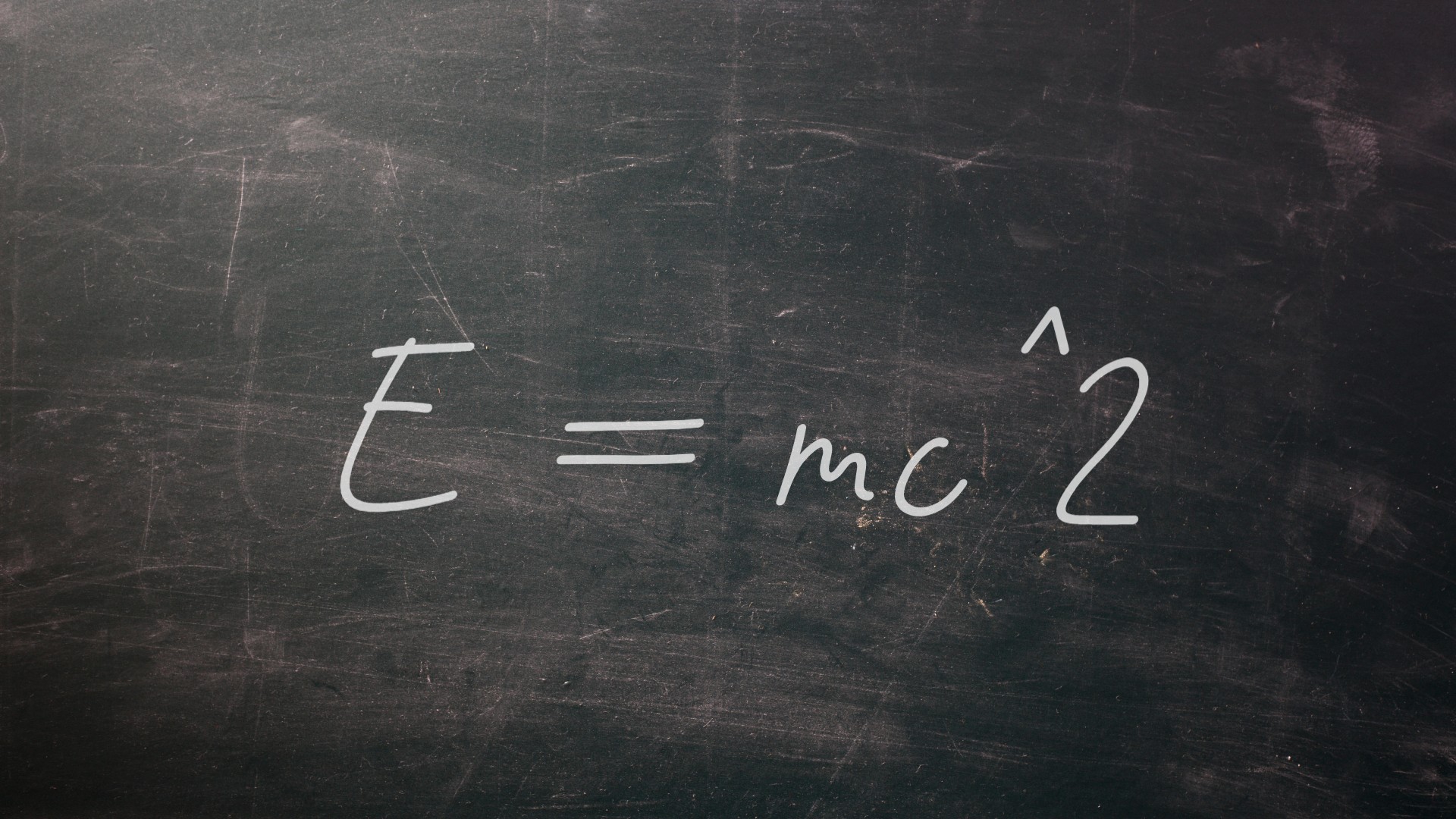
No list of transformational equations could be complete without the most famous equation of all. First stated by Albert Einstein in 1905 as part of his groundbreaking theory of special relativity, E = mc^2 showed that matter and energy were two aspects of one thing. In the equation, E stands for energy, m represents mass and c is the constant speed of light. The notions contained within such a simple statement are still hard for many people to wrap their minds around, but without E = mc^2, we wouldn't understand how stars or the universe worked or know to build gigantic particle accelerators like the Large Hadron Collider to probe the nature of the subatomic world.
Friedmann's equations
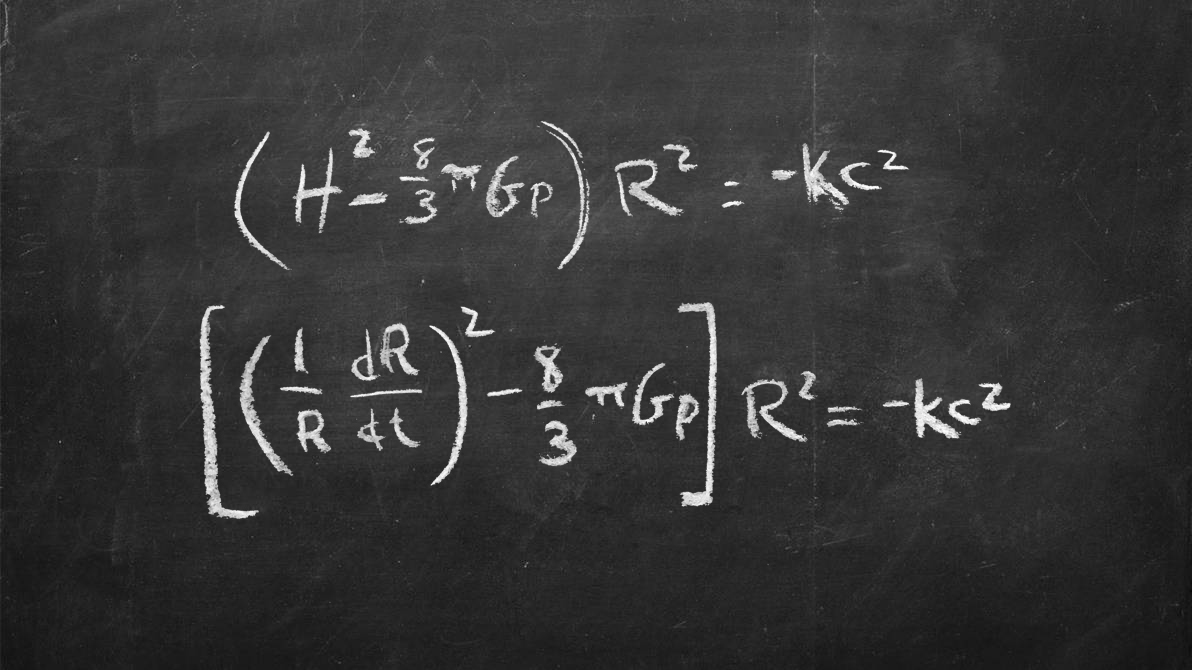
It seems like hubris to think you can create a set of equations that define the entire cosmos, but that's just what Russian physicist Alexander Friedmann did in the 1920s. Using Einstein's theories of relativity, Freidmann showed that the characteristics of an expanding universe could be expressed from the Big Bang onward using two equations.
They combine all the important aspects of the cosmos, including its curvature, how much matter and energy it contains, and how fast it's expanding, as well as a number of important constants, like the speed of light, the gravitational constant and the Hubble constant, which captures the accelerating expansion of the universe. Einstein famously didn't like the idea of an expanding or contracting universe, which his theory of general relativity suggested would happen due to the effects of gravity. He tried to add a variable into the result denoted by the Greek letter lambda that acted counter to gravity to make the cosmos static. While he later called it his greatest mistake, decades afterwards the idea was dusted off and shown to exist in the form of the mysterious substance dark energy, which is driving an accelerated expansion of the universe.
Shannon's information equation
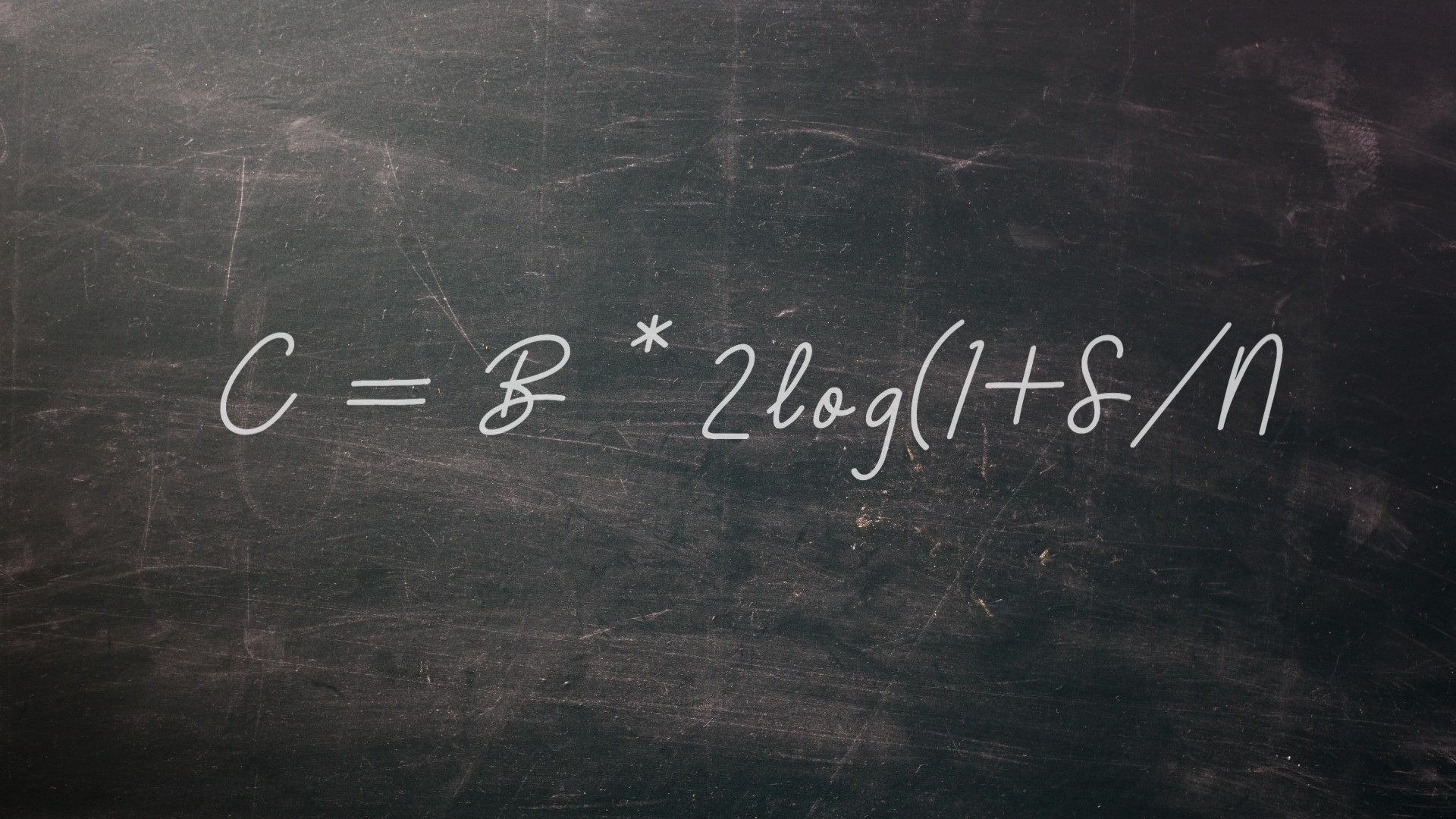
Most people are familiar with the 0s and 1s that make up computer bits. But this critical concept wouldn't have become popular without the pioneering work of American mathematician and engineer Claude Shannon. In an important 1948 paper, Shannon laid out an equation showing the maximum efficiency at which information could be transmitted, often given as C = B * 2log(1+S/N). In the formula, C is the achievable capacity of a particular information channel, B is the bandwidth of the line, S is the average signal power and N is the average noise power. (The S over N gives the famous signal-to-noise ratio of the system.) The output of the equation is in units of bits per second. In the 1948 paper, Shannon credits the idea of the bit to mathematician John W. Tukey as a shorthand for the phrase “binary digit.”
May's logistic map
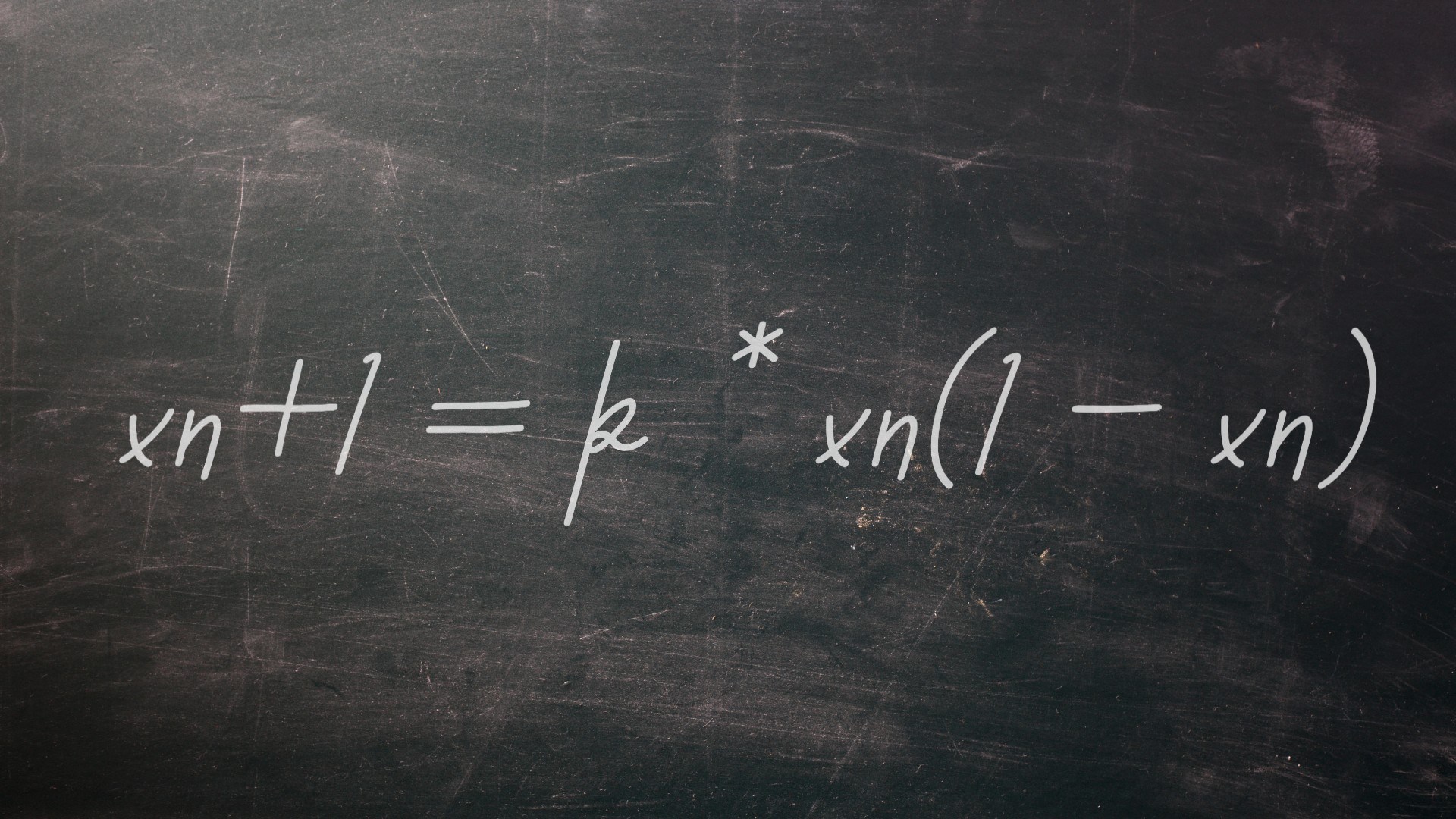
Very simple things can sometimes generate unimaginably complex results. This truism might not seem all that radical, but it took until the mid-20th century for scientists to fully appreciate the idea's weight. When the field of chaos theory took off during that time, researchers began to get a handle on the ways that systems with just a few parts that fed back on themselves might produce random and unpredictable behavior. Australian physicist, mathematician and ecologist Robert May wrote a paper, published in the journal Nature in 1976, titled "Simple mathematical models with very complicated dynamics," which popularized the equation xn+1 = k * xn(1 – xn).
Xn represents some quantity in a system at the present time that feeds back on itself through the part designated by (1 – xn). K is a constant, and xn+1 shows the system at the next moment in time. Though quite straightforward, different values of k will produce wildly divergent results, including some with complex and chaotic behavior. May's map has been used to explain population dynamics in ecological systems and to generate random numbers for computer programming.
