Why does E=mc^2?

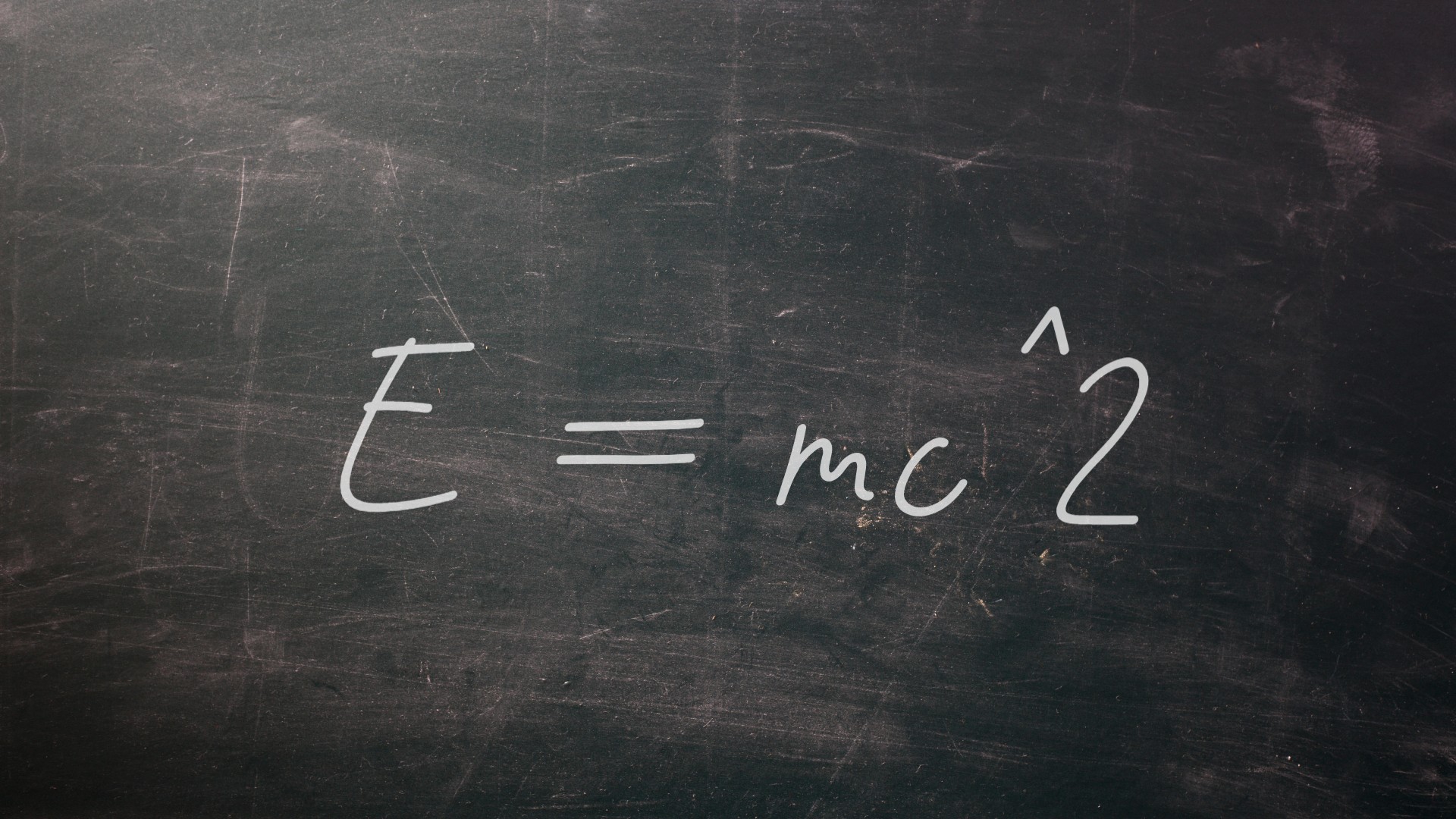
The famous equation E = mc^2, derived by Einstein, means that energy is equal to mass times the speed of light squared. Equivalently, it also means that any amount of mass is equal to energy divided by the speed of light squared. This little equation is central to the theory of special relativity, and also explains how nuclear fusion and fission can generate energy.

Who said E = mc^2?

In a famous paper written in 1905, Albert Einstein discovered an equality between mass and energy. He found that the conservation of mass (a famous and important law in physics) is the same as the conservation of energy, and vice versa. These insights were a part of his development of the theory of special relativity, which describes the relativity of motion, particularly at near light speed. Although Einstein didn't write exactly that E = mc^2 in that paper, he did write an equivalent expression that means the same thing, according to educational website Earthsky.org. He later tweaked it to the now-famous formula, according to the American Museum of Natural History.

What does E = mc^2 mean?

One way to understand what E= mc^2 means is to think about the speed of light as simply a number that can be expressed in terms of any arbitrary set of units. If you define your units — for example, what a "meter" and a "second" are — you can say that the speed of light is around 300 million meters per second (or 670 million mph, although we haven't defined a mile and an hour).

Latest Videos From

But it also would be possible to simply define the speed of light as equal to … 1. Just 1. No miles, no seconds, no fortnights, no leagues. Just … 1. Physics allows this because it's just a number, and we're picking a system where speed has no units. In this system, a jet airliner cruises at a snail's pace of 0.000001, or 0.0001% the speed of light. Two of the fastest human-made objects, the Helios probes, zoomed around the solar system at a whopping 0.00025! Look at them go!

Once the speed of light is defined as 1, we can look at the most famous equation in physics: E = mc^2.

We know all the bits, but let's refresh: E is for energy, m is for mass and c is the constant speed of light. But in this newly defined unit system (called geometrized units), c equals 1, and that famous equation boils down to its essence:

E = m.

In other words, Energy = mass.

It doesn't get any clearer than that. Energy is mass. Mass is energy. They are equivalent. They are the same thing, according to Union University.

What is the full equation?

What about light? Photons, or packets of light, don't have any mass, but they have lots of energy. 

It's true that photons don't have mass. But they do have momentum, which is how things like light sails (also called solar sails) get the oomph they need to glide around the solar system: Their propulsion comes from the sun's radiation pressure. And momentum has energy. But where's the momentum in E = m? It looks like there aren't enough letters to account for it.

The confusion comes from the m used in E = m. People normally think of mass as something concrete and simple. Hold a rock; it has mass. Throw it, and it has mass and momentum. But that's not the m in E = m. Instead, when Einstein wrote down that equation, he meant something different, usually referred to as relativistic mass.

That term isn't used so much nowadays because it causes so much head-scratching. But what did Einstein mean by it?.

According to the most basic understanding of special relativity, "it's impossible to move at the speed of light, because the faster something goes, the more mass it has. To get to the speed of light, something has to have infinite mass, so it would be impossible to push!" A fundamental aspect of the universe is that there's a universal speed limit: the same speed light goes. No matter what, no one can crack that speed. 

Here's how that concept plays out in practice:

Let's say I give you a nice, solid shove, which sends you flying away at 0.9 — that is, 90% the speed of light. If I catch up to you and give you the exact same shove, again, you won't be going 180% the speed of light, because that's not allowed. You'll get closer to the speed of light, but you'd never cross it. So, for the exact same force of that shove, I don't move you as fast. I get less bang for my buck.

And the closer you get to the speed of light, the less effective each shove will be: The first one may get you to 0.9, then the second to 0.99, then 0.999, then 0.9999. In fact, it's as if you were getting more massive. That's exactly what more mass means: You get harder to push.

So, what's going on? The answer is energy. You still have the same old rest mass you always had. But you're going really, really fast. And that speed has an energy associated with it — kinetic energy. So it's like all that kinetic energy is acting like extra mass; any way I count it, you get harder to push because of that fundamental speed limit.

In other words, energy is mass. Now, back to the m in E = m. When physicists first started playing with those equations, they were well aware of the universal speed limit and its nonintuitive consequence that you get harder to push the faster you go. So they encapsulated that concept into a single variable: the relativistic mass, which combines both the normal, everyday mass and the "effective" mass gained from having loads of kinetic energy.

When we break up m into its different parts, we get this equation, where p is momentum:

E2 = m2 + p2

Or, bringing back c, the speed of light, we get this:

E2 = m2c4 + p2c2

That's why photons don't have mass — but they do have momentum, so they still get energy, according to the University of Illinois at Urbana-Champaign Department of Physics.

Why is E = mc^2 true?

One way to think about this relationship is to consider that stationary objects are still moving — in time, that is. A rock, for example,may be perfectly still. But it's still moving into the future, at the rate of 1 second per second. The same is true for every other object in the universe.

While people are familiar with kinetic energy — the energy of motion — they usually define that motion only in terms of movement through space. But relativity considers motion through the entire four-dimensional fabric of space-time. Something that is perfectly still in space is still moving through time, so we can associate a kinetic energy with that motion. 

This is what leads to E = mc^2: the energy of a stationary (in space) object that is nonetheless moving through time, physicist and blogger Chad Orzel wrote for Forbes. 

Why is E = mc^2 important?

Mass is a kind of energy. But energy acts like mass. So what's the deal? Are we just talking in circles?

No. Mass is energy. Energy is mass. You can count things energy-wise or mass-wise. It doesn't matter. They're the same thing.

A hot cup of coffee literally weighs more than a cold cup. A fast-moving spaceship literally weighs more than a slow one. An atomic nucleus is a compact, bundled-up ball of energy, and sometimes we can tease some of that energy out for a big boom: a nuclear reaction.

Additional resources

Check out this excellent video on the deeper meaning behind Einstein's famous equation, from PBS Space Time. You can also listen to this podcast episode that digs into the topic, or check out this video created by Fermilab discussing the full equation.

Bibliography

Cox, B. and Forshaw J. “Why Does E=mc2?” (De Capo Press 2009)

Morris, D. “The Special Theory of Relativity” (Mercury Learning and Information 2016)

Freund, J. “Special Relativity for Beginners” (World Scientific 2008)

Smith, J. “Introduction to Special Relativity” (Courier Corporation 1995)

Einstein, A. “Relativity: The Special and General Theory” (Hartsdale House 1921)

This article was originally published on Live Science on May 24, 2016, and was rewritten on July 26, 2022.