What is the Fibonacci sequence?
From its origins to its significance, almost every popular notion about the famous Fibonacci sequence is wrong.

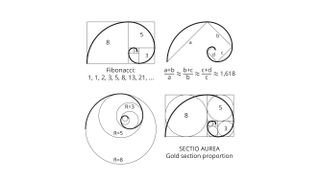
The Fibonacci sequence is a series of numbers in which each number is the sum of the two that precede it. Starting at 0 and 1, the first 10 numbers of the sequence look like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on forever. The Fibonacci sequence can be described using a mathematical equation: Xn+2= Xn+1 + Xn
People claim there are many special properties about the numerical sequence, such as the fact that it is “nature’s secret code” for building perfect structures, like the Great Pyramid at Giza or the iconic seashell that likely graced the cover of your school mathematics textbook. But much of that is incorrect and the true history of the series is a bit more down-to-earth.
Who discovered the Fibonacci sequence?
The first thing to know is that the sequence is not originally Fibonacci's, who in fact never went by that name. The Italian mathematician who we call Leonardo Fibonacci was born around 1170, and originally known as Leonardo of Pisa, said Keith Devlin, a mathematician at Stanford University.
Only in the 19th century did historians come up with the nickname Fibonacci (roughly meaning, "son of the Bonacci clan"), to distinguish the mathematician from another famous Leonardo of Pisa, Devlin said.
Keith Devlin is an emeritus mathematician at Stanford University, a co-founder and executive director emeritus of the Stanford H-STAR institute, a co-founder of the Stanford mediaX research network, and a senior researcher emeritus at the Center for the Study of Language and Information. He is a World Economic Forum fellow, a fellow of the American Association for the Advancement of Science, and a fellow of the American Mathematical Society. He has written 33 books and over 80 research articles.
Read more: Large Numbers that Define the Universe
Leonardo of Pisa did not actually discover the sequence, said Devlin, who is also the author of "Finding Fibonacci: The Quest to Rediscover the Forgotten Mathematical Genius Who Changed the World," (Princeton University Press, 2017). Ancient Sanskrit texts that used the Hindu-Arabic numeral system first mention it in 200 B.C. predating Leonardo of Pisa by centuries.
"It's been around forever," Devlin told Live Science.

However, in 1202 Leonardo of Pisa published the massive tome "Liber Abaci," a mathematics "cookbook for how to do calculations," Devlin said. Written for tradesmen, "Liber Abaci" laid out Hindu-Arabic arithmetic useful for tracking profits, losses, remaining loan balances and so on, he added.
In one place in the book, Leonardo of Pisa introduces the sequence with a problem involving rabbits. The problem goes as follows: Start with a male and a female rabbit. After a month, they mature and produce a litter with another male and female rabbit. A month later, those rabbits reproduce and out comes — you guessed it — another male and female, who also can mate after a month. (Ignore the wildly improbable biology here.) After a year, how many rabbits would you have?
The answer, it turns out, is 144 — and the formula used to get to that answer is what's now known as the Fibonacci sequence.
Read more: 9 equations that changed the world
"Liber Abaci" first introduced the sequence to the Western world. But after a few scant paragraphs on breeding rabbits, Leonardo of Pisa never mentioned the sequence again. In fact, it was mostly forgotten until the 19th century, when mathematicians worked out more about the sequence's mathematical properties. In 1877, French mathematician Édouard Lucas officially named the rabbit problem "the Fibonacci sequence," Devlin said.
Why is the Fibonacci sequence important?
Other than being a neat teaching tool, the Fibonacci sequence shows up in a few places in nature. However, it's not some secret code that governs the architecture of the universe, Devlin said.
It's true that the Fibonacci sequence is tightly connected to what's now known as the golden ratio, phi, an irrational number that has a great deal of its own dubious lore. The ratio of successive numbers in the Fibonacci sequence gets ever closer to the golden ratio, which is 1.6180339887498948482...
Read more: The 9 most massive numbers in existence
The golden ratio manages to capture some types of plant growth, Devlin said. For instance, the spiral arrangement of leaves or petals on some plants follows the golden ratio. Pinecones exhibit a golden spiral, as do the seeds in a sunflower, according to "Phyllotaxis: A Systemic Study in Plant Morphogenesis" (Cambridge University Press, 1994). But there are just as many plants that do not follow this rule.
"It's not 'God's only rule' for growing things, let's put it that way," Devlin said.
Are there real-life examples of the Fibonacci sequence?
Perhaps the most famous example of all, the seashell known as the nautilus, does not in fact grow new cells according to the Fibonacci sequence, he added. When people start to draw connections to the human body, art and architecture, links to the Fibonacci sequence go from tenuous to downright fictional.
"It would take a large book to document all the misinformation about the golden ratio, much of which is simply the repetition of the same errors by different authors," George Markowsky, a mathematician who was then at the University of Maine, wrote in a 1992 paper in the College Mathematics Journal.
Much of this misinformation can be attributed to an 1855 book by the German psychologist Adolf Zeising called "Aesthetic Research." Zeising claimed the proportions of the human body were based on the golden ratio. In subsequent years, the golden ratio sprouted "golden rectangles," "golden triangles" and all sorts of theories about where these iconic dimensions crop up.
Since then, people have said the golden ratio can be found in the dimensions of the Pyramid at Giza, the Parthenon, Leonardo da Vinci's "Vitruvian Man" and a bevy of Renaissance buildings. Overarching claims about the ratio being "uniquely pleasing" to the human eye have been stated uncritically, Devlin said. All these claims, when they're tested, are measurably false, he added.
"We're good pattern recognizers. We can see a pattern regardless of whether it's there or not," Devlin said. "It's all just wishful thinking."
Editor's note: Adam Mann contributed to this article.
Originally published on Live Science.
Sign up for the Live Science daily newsletter now
Get the world’s most fascinating discoveries delivered straight to your inbox.

Tia is the managing editor and was previously a senior writer for Live Science. Her work has appeared in Scientific American, Wired.com and other outlets. She holds a master's degree in bioengineering from the University of Washington, a graduate certificate in science writing from UC Santa Cruz and a bachelor's degree in mechanical engineering from the University of Texas at Austin. Tia was part of a team at the Milwaukee Journal Sentinel that published the Empty Cradles series on preterm births, which won multiple awards, including the 2012 Casey Medal for Meritorious Journalism.
