What is time dilation?
Einstein realized that time is relative and passes at different rates for different people.

Time dilation refers to the seemingly odd fact that time passes at different rates for different observers, depending on their relative motion or positions in a gravitational field.
Here’s how that works. Time is relative. As counterintuitive as that sounds, it's a consequence of Einstein's theory of relativity. In everyday life, we're used to speed being relative — so, for example, a car traveling at 60 mph (97 km/h) relative to a stationary observer would be seen as moving at 120 mph (193 km/h) by a driver going in the opposite direction at the same speed.
This same phenomenon also impacts time. Depending on an observer’s relative motion or their position within a gravitational field, that observer would experience time passing at a different rate than that of another observer. This effect, known as time dilation, becomes detectable only under certain conditions, although at a low level, we're subject to it all the time. Let's take a closer look at the theory of time dilation and some of its consequences, including GPS errors and the famous twin paradox.
Time dilation defined
Time dilation is the slowing of time as perceived by one observer compared with another, depending on their relative motion or positions in a gravitational field. It's a consequence of Einsteinian relativity, in which time is not as absolute as it might appear; the rate at which it passes is different for observers in different frames of reference.
Einstein's starting point was the fact that light always has the same measured speed regardless of the observer's own motion, according to the late Michigan State University physics professor Jon Pumplin. This seemingly innocuous assumption inevitably leads to the conclusion that "moving clocks run slowly." This phrase is often used as a concise description of time dilation, but it's somewhat misleading because of the emphasis it places on clocks, which are only relevant insofar as we use them to measure time. But we really ought to think of time dilation as "an unexpected truth about space and time, rather than as a property of the clock," Pumplin argued.
Time dilation and the speed of light

The theory of relativity has two parts — special relativity and general relativity — and time dilation features in both. The principle that the speed of light is the same for all observers plays a key role in special relativity. One of its consequences, according to Boston University physicist Andrew Duffy, is that two observers moving at a constant speed relative to each other measure different times between the same events. But the effect becomes noticeable only at velocities approaching the speed of light, commonly symbolized by c.
Imagine a spaceship traveling at 95% of the speed of light to a planet 9.5 light-years away. A stationary observer on Earth would measure the journey time as distance divided by speed, or 9.5/0.95 = 10 years. The spaceship crewmembers, on the other hand, experience time dilation and thus perceive the trip as taking only 3.12 years. (The math here is a little more complicated, but we'll get to it later.) In other words, between leaving Earth and reaching their destination, the crewmembers age a little over three years, while 10 years have passed for people back on Earth.
Although really striking situations like this call for enormously high speeds, time dilation occurs on a more modest scale for any kind of relative motion. For example, a regular flier who crosses the Atlantic every week would have experienced about a thousandth of a second less time than a non-traveler after 40 years, according to "How to Build a Time Machine" (St. Martin's Griffin, 2013). The book also explains how the kind of speeds needed for more impressive feats of time dilation can occur in the real world, at least in the case of short-lived elementary particles called muons. These are created when cosmic rays hit Earth's upper atmosphere, and they can travel at nearly the speed of light. The muons are so unstable that they shouldn't last long enough to reach Earth's surface, yet many of them do. That's because time dilation can extend their lifetimes by a factor of five.
Time dilation and gravity
Ten years after he postulated special relativity, Einstein expanded his theory to include gravitational effects in general relativity. But time dilation in this theory depends not on the speed of travel but the strength of the local gravitational field. We already live in a moderate gravitational field on Earth's surface, so it turns out, we're subject to time dilation without realizing it. Furthermore, the strength of the effect varies as we move up and down within Earth's field.
Gravity is slightly weaker on the top floor of a high building than at ground level, so the time dilation effect is also weaker higher up. Time goes faster the farther away you are from Earth's surface. Even though the effect is too small to detect with human senses, the time difference between different altitudes can be measured using extremely accurate clocks, as West Texas A&M University physics professor Christopher Baird describes on his website.
To see a more dramatic example of gravitational time dilation, we need to find somewhere with much stronger gravity than Earth, such as the neighborhood around a black hole. NASA has considered what would happen if a clock were put in orbit 6 miles (10 kilometers) from a black hole having the same mass as the sun. It turns out that when viewed through a telescope from a safe distance, the clock would take around an hour and 10 minutes to show a difference of 1 hour.
Time dilation equation
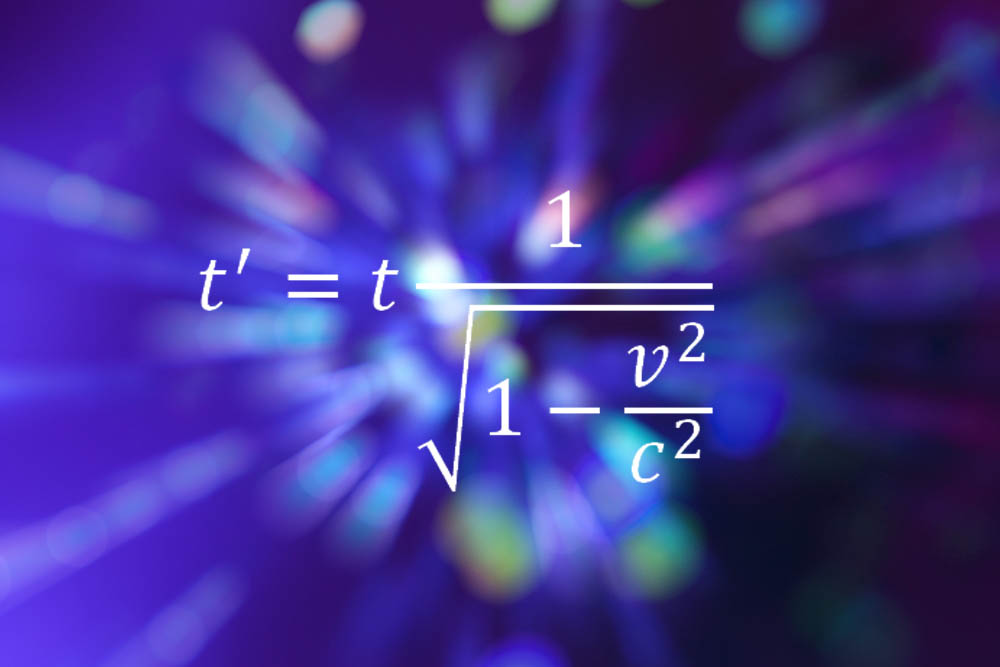
Einstein's original time dilation equation is based on special relativity. As daunting as the equation looks at first glance, it's not that difficult if we have a scientific calculator and work through the formula step by step. First, take the speed v of the moving object and divide it by c, the speed of light, and square the result. This should give you a number somewhere between 0 and 1. Subtract this from 1, and take the square root; then invert the result. You should be left with a number greater than 1, which is the ratio of the time interval as measured by a stationary observer to that of the moving observer.
If that sounds like too much work, you can use an online calculator provided by Georgia State University. Just type in the speed, v, as a fraction of c, and the corresponding time ratio will appear automatically. The same website also has the analogous formula relating to gravitational time dilation.
Time dilation in space

Time dilation is of double relevance to spacecraft, due both to their high speeds and the changing gravitational fields they experience. In 2020, a group of students at the University of Leicester in the U.K. computed the time dilation effects on NASA's Voyager 1 probe in the 43 years following its launch in 1977. Special relativity predicted that Voyager has aged 2.2 seconds less than we have on Earth. But general relativity partially counterbalances this. We experience stronger gravity than the spacecraft, so in this sense, the probe has aged around 1 second more than we have. Combining the two effects, Voyager still turns out to be younger than Earthlings, but by only about 1.2 seconds.
Calculations like these may seem frivolous, but they can be very important in situations in which precise timing is critical. In the case of the GPS satellites used for navigation, for example, timing errors of just a few nanoseconds (billionths of a second) can lead to a positioning error of hundreds of meters, which is clearly unacceptable if you're trying to pinpoint a specific address. To achieve the desired accuracy, the GPS system has to account for time dilation, which can amount to 38 microseconds (millionths of a second) per day, according to Richard W. Pogge, a distinguished professor of astronomy at The Ohio State University. As in the Voyager example, both special and general relativity contribute to this figure, with 45 microseconds coming from gravitational time dilation and minus 7 microseconds from the speed-related effect.
The twin paradox
One of the most mind-bending consequences of time dilation is the so-called twin paradox. In this thought experiment, one identical twin lives on Earth while their twin takes a round trip to a distant star at velocities approaching the speed of light. When they meet up again, the traveling twin — thanks to time dilation of the special relativistic kind — has aged far less than the one who stayed at home. The apparent "paradox" comes from the mistaken belief that the situation is symmetrical — in other words, that you could also say the traveling twin is stationary relative to the Earthbound twin, meaning that the Earthling would have aged less than the star-voyaging twin. .
But that's not the case, because the situation isn't symmetrical. When special relativity talks about relative motion, it's referring to motion at constant speed in a straight line. That's not the case here. Because the twins are together at the start and end of the journey, the traveler has to accelerate from a standstill to top speed and then, at some point, turn around and head back in the opposite direction, before eventually decelerating to a stop again. These phases of acceleration and deceleration bring in general relativity, because they have similar effects to a gravitational field, according to "Paradox: The Nine Greatest Enigmas in Physics"(Crown, 2012). When the math is worked out to account for this acceleration, it turns out that, in something akin to time travel, the spacefaring twin does indeed age more slowly than the Earthbound one.
Additional time dilation resources
- See this video from NASA: Why clocks in motion slow down according to relativity theory
- Read more about the twin paradox, from the Max Planck Institute for Gravitational Physics.
- Learn more about how relativity is essential for a working universe in "The Reality Frame" (Icon Books, 2017).
Originally published on Live Science.
Get the world’s most fascinating discoveries delivered straight to your inbox.

Andrew May holds a Ph.D. in astrophysics from Manchester University, U.K. For 30 years, he worked in the academic, government and private sectors, before becoming a science writer where he has written for Fortean Times, How It Works, All About Space, BBC Science Focus, among others. He has also written a selection of books including Cosmic Impact and Astrobiology: The Search for Life Elsewhere in the Universe, published by Icon Books.
