Archimedes was possibly the world's greatest scientist — at least the greatest in the classical age. He was a physicist, mathematician, astronomer, inventor and engineer. Many of his inventions, theories and concepts are still in use today. Perhaps his best-known achievement was his "Eureka" moment, when he discovered the principle of buoyancy.
Biography
Archimedes lived in Syracuse on the island of Sicily in the third century B.C. At that time, Syracuse was one of the most influential cities of the ancient world, according to Scientific American. Trading vessels from Egypt, Greece and Phoenicia filled the city-state's harbor. It was also a hub of commerce, art and science, according to the Archimedes Palimpsest.
After studying geometry and astronomy in Alexandria, the "greatest intellectual center in the ancient world," according to Scientific American, Archimedes settled down in Syracuse to pursue a life of thought and invention.
One of his inventions was the Archimedes screw. This device uses a corkscrew with a hollow tube. When the screw turns, water is pulled up the tube. It was originally used to empty sea water from a ship's hull. It is still used today as a method of irrigation in developing countries, according to the Archimedes Palimpsest.
Archimedes famously said, "Give me a lever and a place to stand, and I'll move the world." This boastful claim expresses the power of leverage, which, at least figuratively, moves the world. Archimedes realized that in order to accomplish the same amount or work, one could make a trade-off between force and distance using a lever. His Law of the Lever states, "Magnitudes are in equilibrium at distances reciprocally proportional to their weights," according to "Archimedes in the 21st Century," a virtual book by Chris Rorres at New York University.
Archimedes also devised defenses for Syracuse against invading armies. He strengthened the walls of Syracuse and constructed war machines. His works held off the Romans for two years. However, in 212 B.C., forces under General Marcellus overtook the city.
Marcellus had respect for Archimedes and sent soldiers to get him so he could meet the famous mathematician. According to the Archimedes Palimpsest, he was so focused on solving a mathematical problem that he did not know the Romans had stormed the city. When a soldier told him to accompany him to see the general, Archimedes told him to go away. The enraged soldier struck him down. Marcellus ordered that Archimedes be buried with honors. Archimedes' tombstone was engraved with the image of a sphere within a cylinder, illustrating one of his geometrical treatises.
'Eureka! Eureka!'
Archimedes has gone down in history as the guy who ran naked through the streets of Syracuse shouting "Eureka!" — or "I have it!" in Greek. The story behind that event was that Archimedes was charged with proving that a new crown made for Hieron, the king of Syracuse, was not pure gold as the goldsmith had claimed. The story was first written down in the first century B.C. by Vitruvius, a Roman architect.
Archimedes thought long and hard but could not find a method for proving that the crown was not solid gold. Soon after, he filled a bathtub and noticed that water spilled over the edge as he got in and he realized that the water displaced by his body was equal to the weight of his body. Knowing that gold was heavier than other metals the crown maker could have substituted in, Archimedes had his method to determine that the crown was not pure gold. Forgetting that he was undressed, he went running naked down the streets from his home to the king shouting "Eureka!"
The Archimedes principle
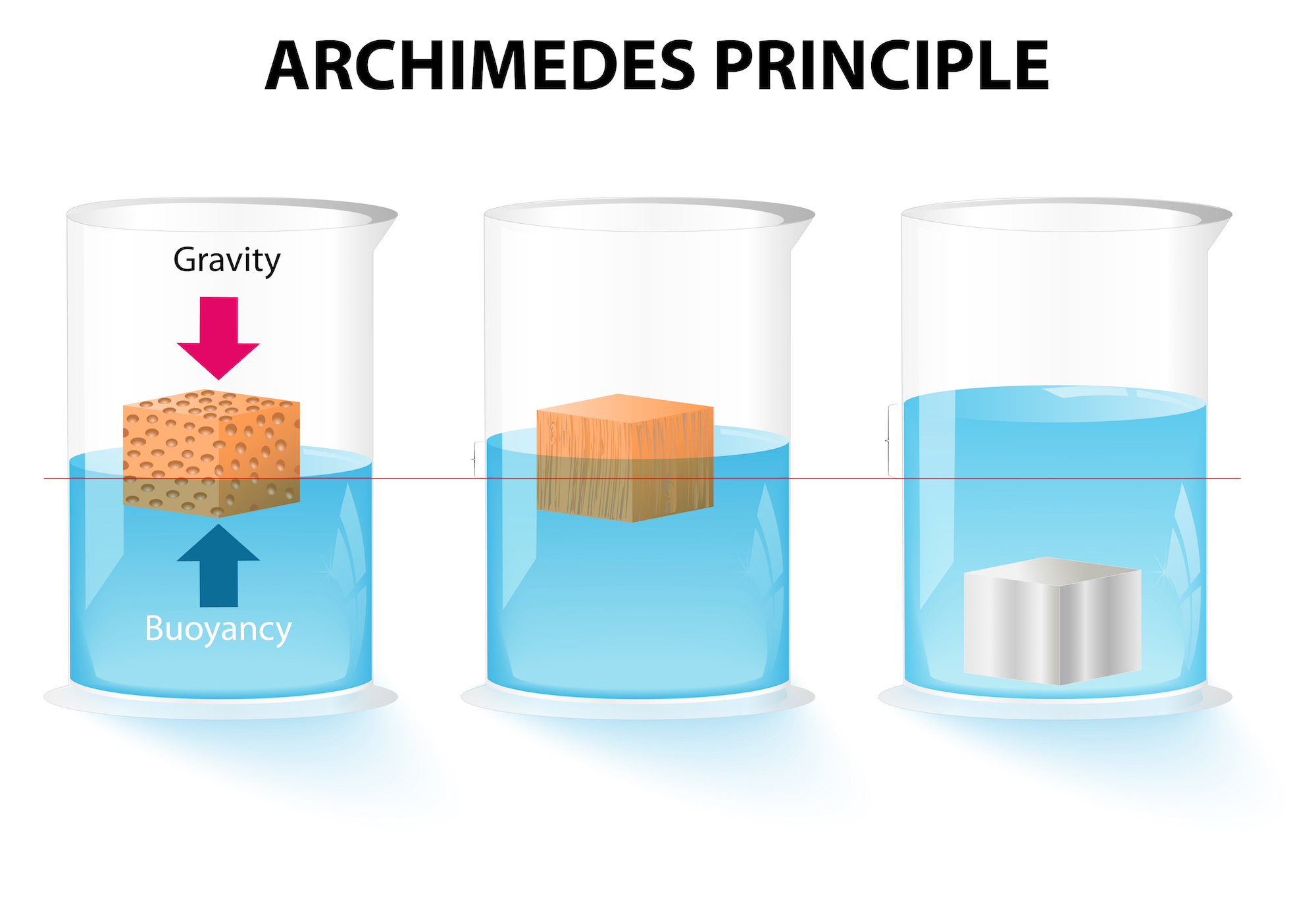
According to Boundless, the Archimedes principle states that the buoyant force on an object submerged in a fluid is equal to the weight of the fluid that is displaced by that object.
If a glass is filled to the top with water and then ice cubes are added to it, what happens? Just like the water spilled over the edge when Archimedes entered his bathtub, the water in the glass will spill over when ice cubes are added to it. If the water that spilled out were weighed (weight is a downward force), it would equal the upward (buoyant) force on the object. From the buoyant force, the volume or average density of the object can be determined.
Archimedes was able to determine that the crown was not pure gold due to the volume of the displaced water, because even though the weight of the crown was identical to the weight of the gold that the king gave the crown maker, the volume was different due the various densities of the metals.
Uses of the Archimedes principle
The Archimedes principle is a very useful and versatile tool. It can be useful in measuring the volume of irregular objects, such as gold crowns, as well as explaining the behaviors of any object placed in any fluid. Archimedes' principle describes how ships float, submarines dive, hot air balloons fly, and many others examples, according to Science Clarified. The Archimedes principle is also used in a large variety of scientific research subjects including medical, engineering, entomology, engineering, and geology.
Current research
Bone volumes/densities
The Archimedes principle has many uses in the medical and dentistry field and is used to determine the densities of bones and teeth. In a 1997 paper published in the journal Medical Engineering & Physics, researchers used the Archimedes principle to measure the volume of the inside spongy part of the bone, also known as the cancellous bone. The volume fraction of the cancellous bone can be used in various age and health studies including being an index in aging studies, osteoporosis, bone strength, stiffness, and elasticity studies. Various methods using Archimedes principle were tested in order to increase reproducibility of the measurements: one where the bone was submerged in distilled water, another where the bone was submerged in a water and surfactant solution, and a third where the bone was placed in a sealed container where the changes in gas pressures were recorded.
An article published in 2017 in the journal Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology is similar in nature to the previous article where various methods were used in order to determine the reproducibility, one of which was using Archimedes principle. The Archimedes principle was compared with using cone beam computed tomography (CBCT) to measure the volume of the teeth. The tests comparing the Archimedes principle and CBCT measurements showed that the latter would be an accurate tool in planning dental procedures.
Submarines
A simple, reliable, cost-effective design for a submarine described in a 2014 paper in the journal Informatics, Electronics, and Vision, is based on the Archimedes principle. Submarines, according to the authors, are designed to travel while completely submerged underwater and rely on the Archimedes principle in order to maintain a constant depth. The design of this prototype submarine uses calculations involving the mass, density, and volume of both the submarine and the displaced water in order to determine the size needed of the ballast tank, which will determine the amount of water than can fill it and therefore the depth to which the submarine can dive.
Water-walking bugs
While the Archimedes principle is used in submarine design to help them dive and resurface, it also explains the reason why some bugs can walk on water. In a 2016 study published in Applied Physics Letters, researchers used a method of measuring shadows created by the water striders in order to measure the curvatures in the water surface. These dips can then be used to derive the water volume that was displaced leading to the force used to keep the water-bugs afloat. The authors said there is a great deal of interest in understanding the physics behind the water-walking bugs in order to create biomimetic water-walking robots.
Geology
A paper published in 2012 in Soft Matter describes a more in-depth view of the Archimedes principle, which the authors call the Generalized Archimedes Principle. The Archimedes principle as it is typically used can only be used as an approximation in many instances of studying sedimentation profiles, while the generalized principle can account for phenomena such as denser particles floating on top of a light fluid. The authors' key point lies in the density perturbations that are induced by the particles suspended in the fluid, which is not taken into account in the traditional use of the Archimedes principle, and a new approach to the Archimedes principle is derived.
Additional resources
