12 surprising facts about pi to chew on this Pi Day
On Pi Day (March 14) we celebrate perhaps the most iconic irrational number on Earth. From its ancient origins to the unanswered questions, here are some of the most surprising facts about pi.

Get the world’s most fascinating discoveries delivered straight to your inbox.
You are now subscribed
Your newsletter sign-up was successful
Want to add more newsletters?

Delivered Daily
Daily Newsletter
Sign up for the latest discoveries, groundbreaking research and fascinating breakthroughs that impact you and the wider world direct to your inbox.

Once a week
Life's Little Mysteries
Feed your curiosity with an exclusive mystery every week, solved with science and delivered direct to your inbox before it's seen anywhere else.

Once a week
How It Works
Sign up to our free science & technology newsletter for your weekly fix of fascinating articles, quick quizzes, amazing images, and more

Delivered daily
Space.com Newsletter
Breaking space news, the latest updates on rocket launches, skywatching events and more!

Once a month
Watch This Space
Sign up to our monthly entertainment newsletter to keep up with all our coverage of the latest sci-fi and space movies, tv shows, games and books.

Once a week
Night Sky This Week
Discover this week's must-see night sky events, moon phases, and stunning astrophotos. Sign up for our skywatching newsletter and explore the universe with us!
Join the club
Get full access to premium articles, exclusive features and a growing list of member rewards.
Math nerds everywhere are digging into a slice of pie today to celebrate their most iconic irrational number: pi. After all, March 14, or 3/14, is the perfect time to honor the essential mathematical constant, whose first digits are 3.14.
Pi, or π, is the ratio of a circle's circumference to its diameter. Because it is irrational, it can't be written as a fraction. Instead, it is an infinitely long, nonrepeating number.
But how was this irrational number discovered, and after thousands of years of being studied, does this number still have any secrets? From the number's ancient origins to its murky future, here are some of the most surprising facts about pi.
Related: The 9 most massive numbers in existence
Memorizing pi
The record for the most digits of pi memorized belongs to Rajveer Meena of Vellore, India, who recited 70,000 decimal places of pi over the course of 10 hours on March 21, 2015, according to Guinness World Records. (As of March 2024, Meena still holds this record.) Previously, Chao Lu, of China, who recited pi from memory to 67,890 places in 2005, held the record, according to Guinness World Records.
The unofficial record holder is Akira Haraguchi, who videotaped a performance of his recitation of 100,000 decimal places of pi in 2005, and more recently topped 117,000 decimal places, the Guardian reported.
Number enthusiasts have memorized many digits of pi. Many people use memory aids, such as mnemonic techniques known as piphilology, to help them remember. Often, they use poems written in Pilish (in which the number of letters in each word corresponds to a digit of pi). Speaking of which...
Get the world’s most fascinating discoveries delivered straight to your inbox.
There's a pi "language"
Literary nerds invented a dialect known as Pilish, in which the numbers of letters in successive words match the digits of pi. For example, Mike Keith wrote the book "Not A Wake" (Vinculum Press, 2010) entirely in Pilish:
Now I fall, a tired suburbian in liquid under the trees, Drifting alongside forests simmering red in the twilight over Europe.
("Now" has three letters, "I" has one letter, "fall" has four letters, and so on.)
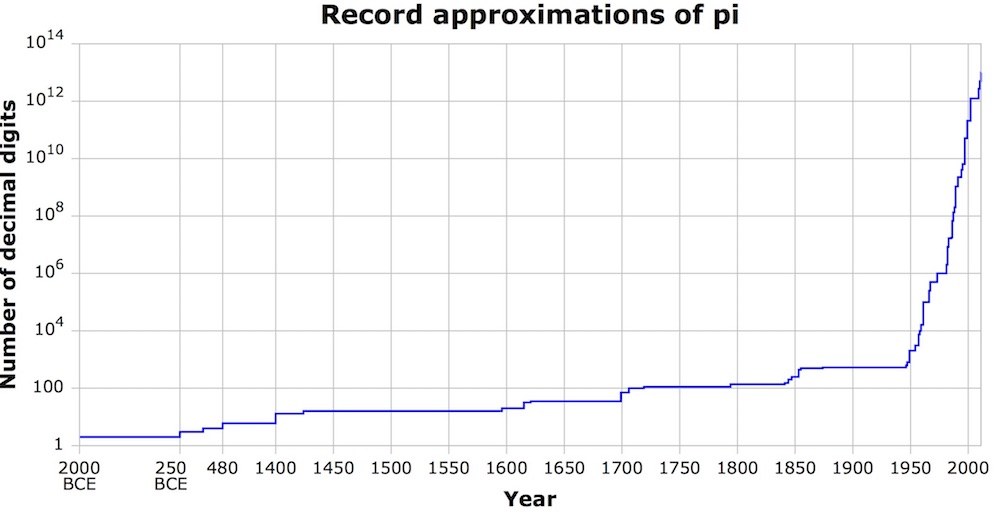
Exponential increase
Because pi is an infinite number, humans will, by definition, never determine every single digit of pi. However, the number of decimal places calculated has grown exponentially since pi's first use. The Babylonians thought the fraction 3 1/8 was good enough in 2000 B.C., while the ancient Chinese and the writers of the Old Testament (Kings 7:23) seemed perfectly happy to use the integer 3. But by 1665, Sir Isaac Newton had calculated pi to 16 decimal places. By 1719, French mathematician Thomas Fantet de Lagny had calculated 127 decimal places, according to "A History of Pi" (St. Martin's Press, 1976).
The advent of computers radically improved humans' knowledge of pi. Between 1949 and 1967, the number of known decimal places of pi skyrocketed from 2,037 on the ENIAC computer to 500,000 on the CDC 6600 in Paris, according to "A History of Pi" (St. Martin's Press, 1976).
Of course, the latest computations blow those early records out of the water.
The most digits of pi ever calculated
In 2021, researchers in Switzerland used a supercomputer to smash the existing record for calculating pi.
Running the supercomupter for 108 days straight, the team calculated pi to more than 62.8 trillion decimal places, blowing past the previous computational record by more than 12 trillion decimal places. That's a lot of pi.
This level of pi precision is unprecedented. However, it may be wasted on one of the world's top science agencies...
NASA only uses 16 digits of pi
How many digits of pi does NASA need to make high-precision calculations about the universe? Way less than you'd think.
According to NASA officials, the space agency rarely needs to use more than 16 digits of pi (or 3.141592653589793) to make accurate calculations about our solar system and its cosmic neighborhood. Using any longer versions of pi start to give severely diminishing returns, according to NASA.
For example: Earth has a diameter of around 7,900 miles (12,700 kilometers), which means its circumference is around 24,900 miles (40,100 km). If you were to calculate this circumference with the first 16 digits of pi and a more accurate version of pi with hundreds of decimal places, the difference between the two answers would be around 300 times less than the width of a human hair, according to NASA.
When looking at the scale of the entire universe, larger versions of pi can be useful, the agency added. But with most of the interesting space action happening within our solar system, NASA rarely needs to go bigger than 3.141592653589793.
Hand-calculating pi
Those who are hoping to calculate pi using an old-fashioned technique can accomplish the task using a ruler, a can and a piece of string, or a protractor and a pencil. The downside of the can method is that it requires a can that is actually round, and the accuracy is limited by how well a person can loop string around its circumference. Similarly, drawing a circle with a protractor and then measuring its diameter or radius with a ruler involves a fair amount of dexterity and precision.
A more precise option is to use geometry. Break up a circle into multiple segments (such as eight or 10 pizza slices). Then, calculate the length of a straight line that would turn the slice into an isosceles triangle, which has two sides of equal length. Adding up all the sides yields a rough approximation for pi. The more slices you create, the more accurate the approximation of pi will be.
Discovery of pi
The ancient Babylonians knew of pi's existence nearly 4,000 years ago. A Babylonian tablet from between 1900 B.C. and 1680 B.C. calculates pi as 3.125, and the Rhind Mathematical Papyrus of 1650 B.C., a famous Egyptian mathematical document, lists a value of 3.1605. The King James Bible (I Kings 7:23) gives an approximation of pi in cubits, an archaic unit of length corresponding to the length of the forearm from the elbow to the middle finger tip (estimated at about 18 inches, or 46 centimeters), according to the University of Wisconsin-Green Bay. The Greek mathematician Archimedes (287-212 B.C.) approximated pi using the Pythagorean theorem, a geometric relationship between the length of a triangle's sides and the area of the polygons inside and outside of circles.
Pi rebranded
Prior to the association of the symbol pi with the circle constant, mathematicians had to say a mouthful to even describe the number. One phrase found in the old math books was the Latin phrase "quantitas in quam cum multiflicetur diameter, proveniet circumferencia," which roughly translates to "the quantity which, when the diameter is multiplied by it, yields the circumference," according to History Today.
The irrational number rocketed to fame when Swiss polymath Leonhard Euler used it in 1737 in his disquisitions on trigonometry. But it didn't get its pithier, Greek-symbol name from Euler. The first mention of pi as such occurred in a book by a lesser-known mathematician, William Jones, who used it in 1706 in his book "Synopsis Palmariorum Matheseos." Jones likely used the symbol for pi to denote the periphery of a circle, according to the book "A History of Pi," (St. Martin's Press, 1976).
Is pi normal?
Pi is definitely weird, but is it normal? Though mathematicians have plumbed many of the mysteries of this irrational number, there are still some unanswered questions.
Mathematicians still don't know whether pi belongs in the club of so-called normal numbers — or numbers that have the same frequency of all the digits — meaning that 0 through 9 each occur 10 percent of the time, according to Trueb's website pi2e.ch. In a paper published Nov. 30, 2016, in the preprint journal arXiv, Trueb calculated that, at least based on the first 2.24 trillion digits, the frequency of the numbers 0 through 9 suggest pi is normal. Of course, given that pi has an infinite number of digits, the only way to show this for sure is to create an airtight math proof. So far, proofs for this most famous of irrational numbers has eluded scientists, though they have come up with some bounds on the properties and distribution of its digits.
Pi sounds divine
While scientists don't know whether pi is normal, they have a better understanding of its other traits. Eighteenth-century mathematician Johann Heinrich Lambert proved pi's irrationality by expressing the tangent of x using a continued fraction.
Later, mathematicians showed that pi was also transcendental. In math terminology, transcendental means the number can't be the solution to any polynomial that has rational number coefficients. In other words, there's no finite, root-finding formula that can be used to calculate pi using rational numbers.
Downgrading pi
While many mathletes are enamored with pi, there is a resistance movement growing. Some argue that pi is a derived quantity, and that the value tau (equal to twice pi) is a more intuitive irrational number.
Tau directly relates the circumference to the radius, which is a more mathematically consequential value, Michael Hartl, author of the "Tau Manifesto," previously told Live Science. Tau also works better in trigonometric calculations, so that tau/4 radians corresponds to an angle that sweeps a quarter of a circle, for instance.
Pi likes a party
There wasn’t always a Pi Day (filled with delectably filled pies, of course). In 1988, physicist Larry Shaw launched the pi-partying day at the San Francisco-based Exploratorium science museum. Every year, on March 14 (3/14) staff and visitors walk a circular parade (and yes the diameter of the circle is like pi times its circumference), each holding one of the infinite numbers of pi. But Pi Day didn’t become a national event until 2009, when the House of Representatives passed Resolution 224, "supporting the designation of Pi Day". The goal? An increased interest in math and science. Let the celebrations begin!
Editor's note: An earlier version of this article was updated on March 14, 2024 to include new updates and information. Live Science contributor Tanya Lewis and editor Brandon Specktor contributed to this article.

Tia is the editor-in-chief (premium) and was formerly managing editor and senior writer for Live Science. Her work has appeared in Scientific American, Wired.com, Science News and other outlets. She holds a master's degree in bioengineering from the University of Washington, a graduate certificate in science writing from UC Santa Cruz and a bachelor's degree in mechanical engineering from the University of Texas at Austin. Tia was part of a team at the Milwaukee Journal Sentinel that published the Empty Cradles series on preterm births, which won multiple awards, including the 2012 Casey Medal for Meritorious Journalism.
 Live Science Plus
Live Science Plus