What are centrifugal and centripetal forces?
Learn the key differences between centripetal and centrifugal forces, their real-world applications in physics, and how they shape our understanding of circular motion.

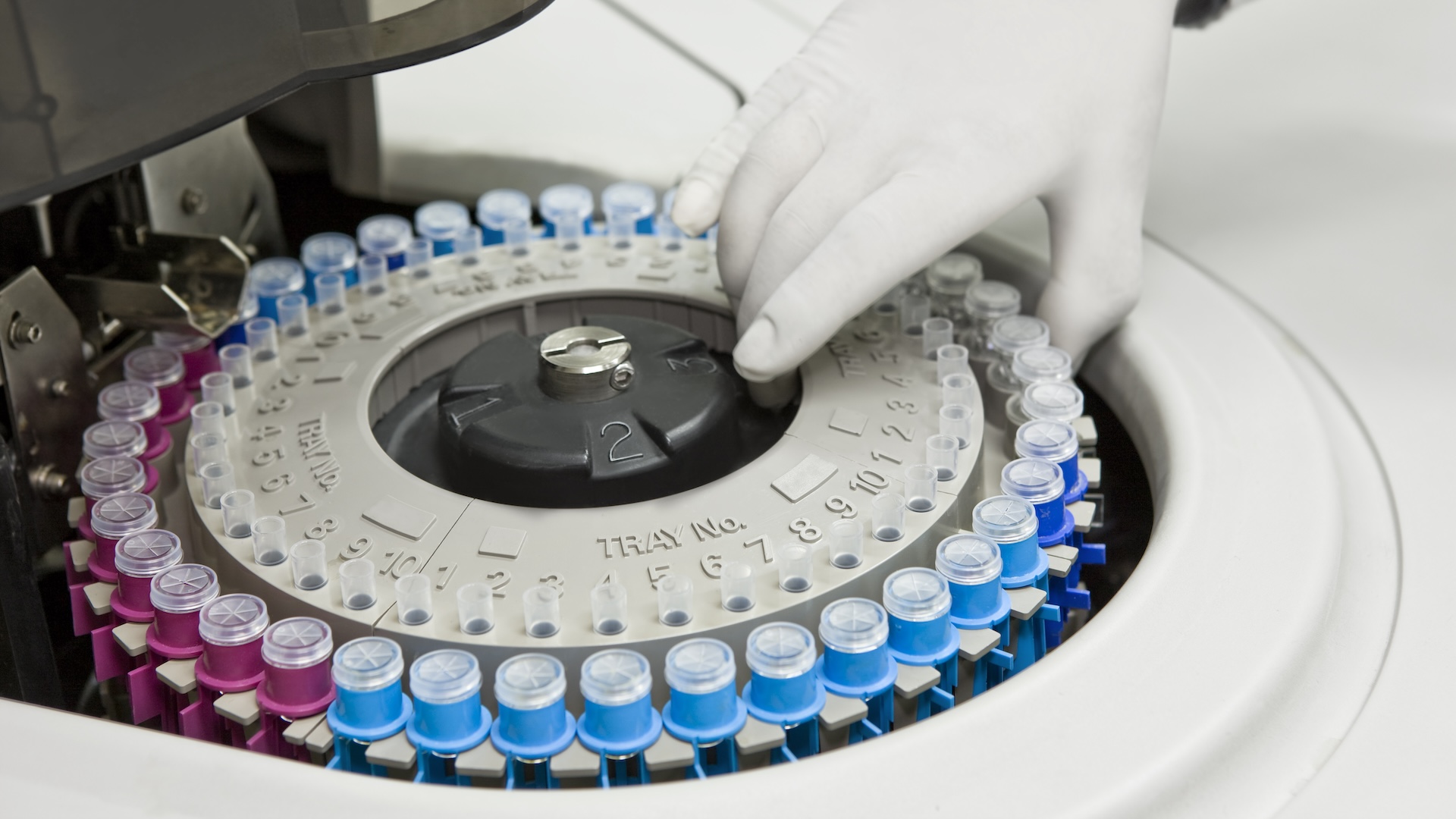
Centripetal and centrifugal forces are two terms used to describe the physics of circular motion — but only one of them is real. The centripetal force keeps an object moving in a circle and is always pointed toward the center of that circle. For instance, the gravitational force of the sun is a centripetal force that keeps Earth orbiting it.
Meanwhile, the centrifugal force is what's known as a fictitious force: It's an apparent outward force on an object that is moving in a circle. This phantom force can nevertheless feel very real if you are the one rotating. For instance, centrifugal force is a way to describe the sensation of flying outward that you get on a Gravitron and similar amusement park rides. Ultimately, these two rotational forces are two sides of the same coin.
"The difference between centripetal and centrifugal force has to do with different 'frames of reference' — that is, different viewpoints from which you measure something," said Andrew A. Ganse, a research physicist previously at the University of Washington. "Centripetal force and centrifugal force are really the exact same force, just in opposite directions because they're experienced from different frames of reference."
If you're outside the rotating system, you would observe the centripetal force. From a rotating object's point of view — say, the laundry spinning in a washing machine — you would experience centrifugal force.
What is the difference between centripetal and centrifugal force?
Centripetal force and centrifugal force are two ways of describing the same thing. The main differences between centripetal and centrifugal forces are the orientation, or direction, of the force and the frame of reference — whether you are tracking the force from a stationary point or from the rotating object's point of view.
The centripetal force points toward the center of a circle, keeping an object moving in a circular path. The word "centripetal" means "center-seeking." The centrifugal force — which, again, is not real — makes it feel, for a rotating object, as if something is pushing it outward, away from the circle's center, according to Christopher S. Baird, an associate professor of physics at West Texas A&M University.
Is centrifugal force real?
While centripetal force is an actual force, centrifugal force is an apparent force. In other words, when you twirl a rock tied on a string, the string exerts an inward centripetal force on the rock, while from the rock's point of view, there appears to be an outward centrifugal force on the string.
If you are observing a rotating system from the outside, you see an inward centripetal force acting to constrain the rotating body to a circular path.
However, if you are whirling around on a Gravitron, you experience an apparent centrifugal force pushing you away from the center of the circle. What you are feeling is the inward centripetal force that is keeping you from going off on a tangent.
Imagine riding in a car taking a banked turn. If you're watching from the outside, you can observe the centripetal force pushing the car inward toward the center, keeping it moving in a circle. But if you're riding inside the car, you instead feel a force pushing you away from the center of the circle — this is the centrifugal force.
What are real-life examples of centripetal and centrifugal force?
A simple real-life example of centripetal force is a rock tied to a string. When the string is swirled around, the tension in that string keeps the rock from flying off in a straight line. That tension points inward, toward the center of the circle.
As another example, the sun's gravity provides the centripetal force that keeps the planets rotating around our central star.
Centrifugal force describes the feeling you get when rounding a corner in a car or when an airplane banks into a turn. Centrifugal force occurs in the spin cycle of a washing machine or when children ride on an amusement park ride.
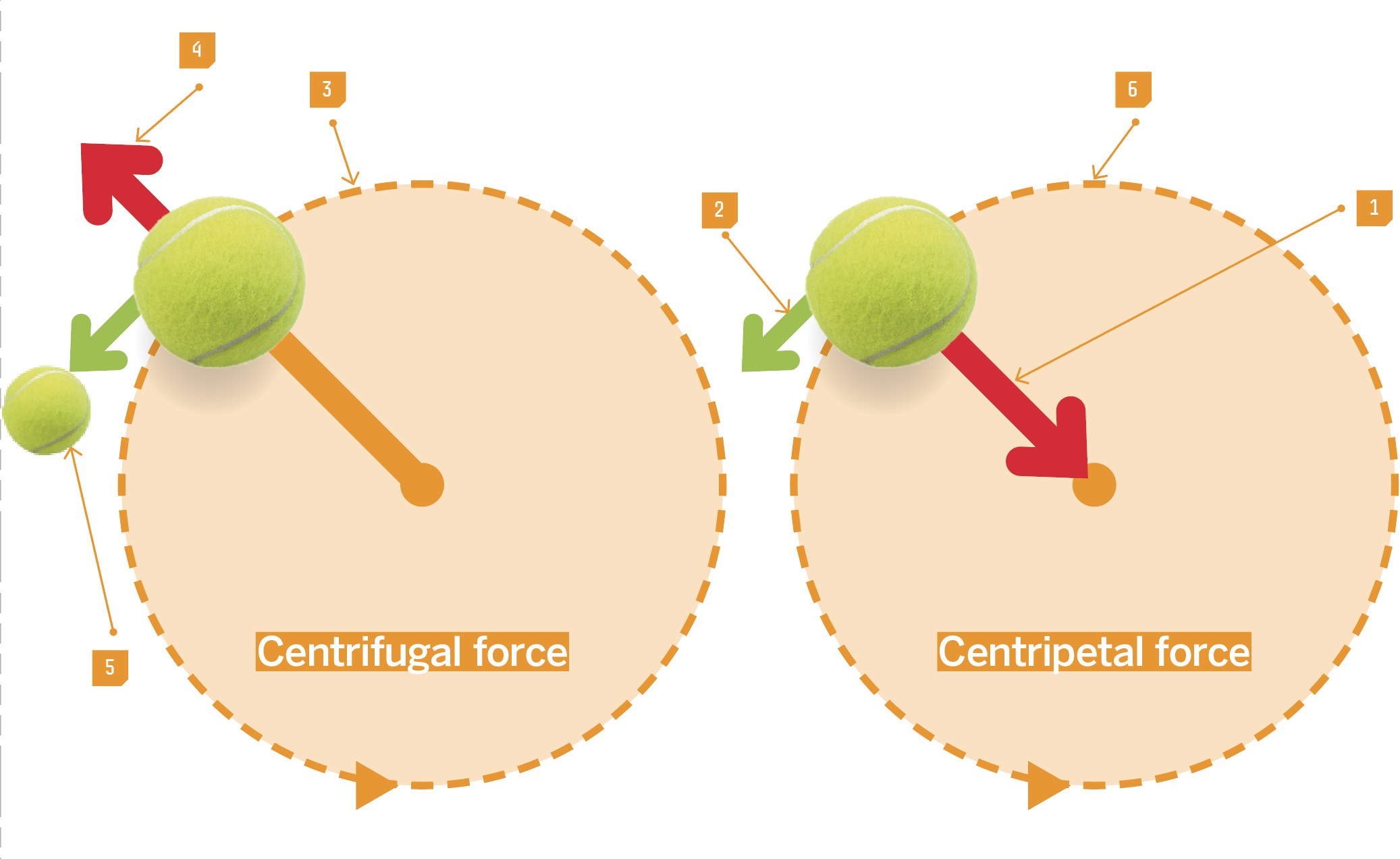
Another practical application of centripetal force is the laboratory centrifuge, which is used to accelerate liquid suspensions. Centrifuges are key tools used in blood sample analysis.
Normally, thermal motion causes continuous mixing, which prevents gravity from forcing blood cells to settle out into different layers. However, a typical laboratory centrifuge can achieve accelerations 600 to 2,000 times that of gravity. This strong acceleration makes heavy red blood cells settle at the bottom of a sample and stratifies the various components of the solution into layers according to their density.
How do you calculate centripetal and centrifugal force?
Centripetal force emerges from Newton's laws of motion. If a massive body is moving through space in a straight line, its inertia will cause it to continue in a straight line unless an outside force causes it to speed up, slow down or change direction.
Here's how centripetal force is calculated:
For the object to follow a circular path without changing speed, a continuous centripetal force must be applied at a right angle to its path. The radius (r) of this circle is equal to the mass (m) times the square of the velocity (v) divided by the centripetal force (F), or r = mv^2/F. The force can be calculated by simply rearranging the equation: F= mv^2/r.
Newton's third law states that "for every action, there is an equal and opposite reaction." Just as gravity causes you to exert a force on the ground, the ground appears to exert an equal and opposite force on your feet. When you are in an accelerating car, the seat exerts a forward force on you just as you appear to exert a backward force on the seat.
In the case of a rotating system, the centripetal force pulls the mass inward to follow a curved path, while the mass appears to push outward due to its inertia. In each of these cases, though, there is only one real force being applied, while the other is only an apparent force.
The formula for centrifugal force is the same as the formula for centripetal force.
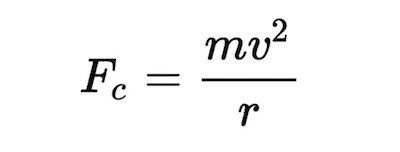
Centripetal force in space exploration
Most things in space move roughly in a circle, so centripetal force plays a big role in space exploration. It governs how satellites orbit our planet, how the moon orbits Earth, and how the rest of the solar system's planets orbit the sun.
This rotational force is also used to simulate the acceleration of a space launch for astronaut training. When a rocket is first launched, it is so laden with fuel and oxidizer that it can barely move. However, as it ascends, it burns fuel at a tremendous rate, continuously losing mass. Newton's second law states that force equals mass times acceleration, or F = ma.
In most situations, mass remains constant. With a rocket, though, its mass changes drastically, while the force — in this case, the thrust of the rocket motors — remains nearly constant. This causes the acceleration toward the end of the boost phase to increase to several times that of normal gravity. NASA uses large, spinning wheels called centrifuges to prepare astronauts for this extreme acceleration. In this application, the centripetal force is provided by the back of the seat pushing inward on the astronaut.
Centrifugal force, meanwhile, could create the illusion of gravity in a future space station. If you rotate a spacecraft via centripetal force, you create an acceleration that will be felt as centrifugal force. This effect can create artificial gravity, assuming the craft spins fast enough.
Learn more about centripetal and centrifugal force
You can read more about the basics of centripetal force from the Swinburne University of Technology. SciShow provides a great video introduction to the topic where they explain and compare centripetal and centrifugal forces. Or you can watch an astronaut describe centripetal force from the International Space Station.
Get the world’s most fascinating discoveries delivered straight to your inbox.

- Tia GhoseEditor-in-Chief (Premium)
 Live Science Plus
Live Science Plus