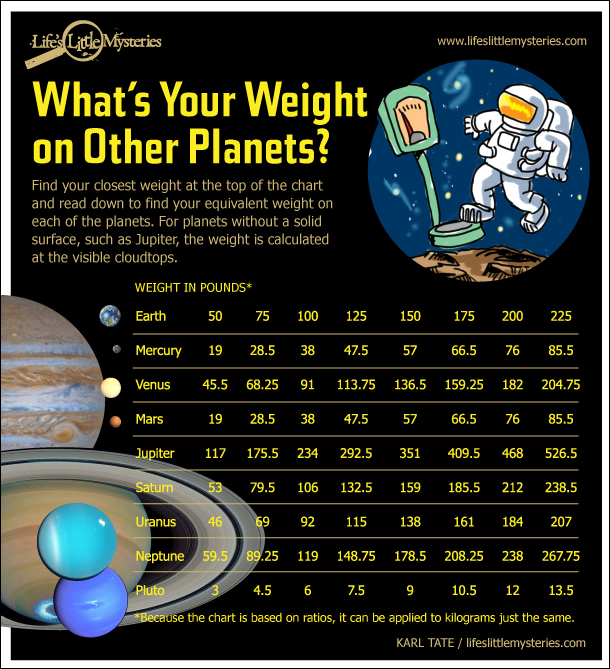
How much would you weigh on other planets?

Whether you are a science fiction fan, a space enthusiast or one of the millions who have watched astronauts gamboling about the moon's surface, you may have wondered how much you would weigh on other planets in the solar system.

To sort this out, it first helps to know a little Physics 101. 

Related: Would humans born on Mars grow taller than Earthlings?

Weight is the force gravity exerts on an object due to its mass. Mass, roughly, measures an object's inertia, its resistance to being moved or stopped, once it's in motion. Your mass remains constant across the universe (except in certain cases discussed in special relativity , but that is another story), while your weight changes depending on the gravitational forces acting on you, which vary from planet to planet.

Newton's Law of Universal Gravitation says that everything that has mass attracts every other thing that has mass, pulling with a force (a) directly proportional to the product of the two objects' masses and (b) inversely proportional to the square of the distance separating their centers.

In other words, although gravity increases linearly as objects grow more massive, it decreases exponentially as the distance between them increases (a phenomenon known as an inverse-square law). When calculating surface gravity, that distance refers to the space separating you (on the surface) from the planet's center of mass. This means that a planet's size actually has a greater relative impact on its gravity and on your weight on its surface than does its mass.

Written as a formula, Newton's gravitation law looks something like this:

F = G((Mm)/r2)

Where

• F is the gravitational force between two objects,
• G is the Gravitational Constant (6.674×10-11 Newtons x meters2 / kilograms2),
• M is the planet's mass (kg),
• m is your mass (kg), and
• r is the distance (m) between the centers of the two masses (the planet's radius).

Without getting too bogged down in the math, we can see that this leads to a surprising result. Take the most massive planet in the solar system, Jupiter, which tips the scales at 316 times the mass of the Earth. You might imagine you would weigh 316 times as much there as here. However, because Jupiter's radius balloons to roughly 11 times as large as Earth's, its gravitational force drops off by a factor of 1/112 at its surface (assuming you could find a way to stand on gas clouds).

However, that does not mean that the proportion of Jupiter's gravity to Earth's is 316 / 112. To calculate the ratio between Earth's surface gravity and that of any other celestial body, you must compute them separately using the formula above, and then divide the desired planet's gravitational force by Earth's. We will spare you the work:

• Mercury: 0.38
• Venus: 0.91
• Earth: 1.00
• Mars: 0.38
• Jupiter: 2.34
• Saturn: 1.06
• Uranus: 0.92
• Neptune: 1.19
• Pluto: 0.06

Because weight = mass x surface gravity, multiplying your weight on Earth by the numbers above will give you your weight on the surface of each planet. If you weigh 150 pounds (68 kg.) on Earth, you would weigh 351 lbs. (159 kg.) on Jupiter, 57 lbs. (26 kg.) on Mars and a mere 9 lbs. (4 kg.) on the dwarf planet of Pluto.

Note that Mercury and Mars have the same proportional gravity, even though Mars is almost twice as massive as Mercury. Mars' superior size, 1.4 times the diameter of Mercury, trumps the effect of its extra mass because of the inverse-square relationship between gravity and distance.

Uranus and Venus present an even more striking example of this phenomenon: Although Uranus lugs around 17.8 times the mass of Venus, its 4.2- times-larger diameter still negates the difference in proportional surface gravity.

Originally published on Live Science.