Dennis Sullivan, mathematician who united chaos theory and geometric spaces, wins prestigious Abel Prize

News
By published

Sullivan will receive more than $860,000 for his achievements in topology and dynamical systems.

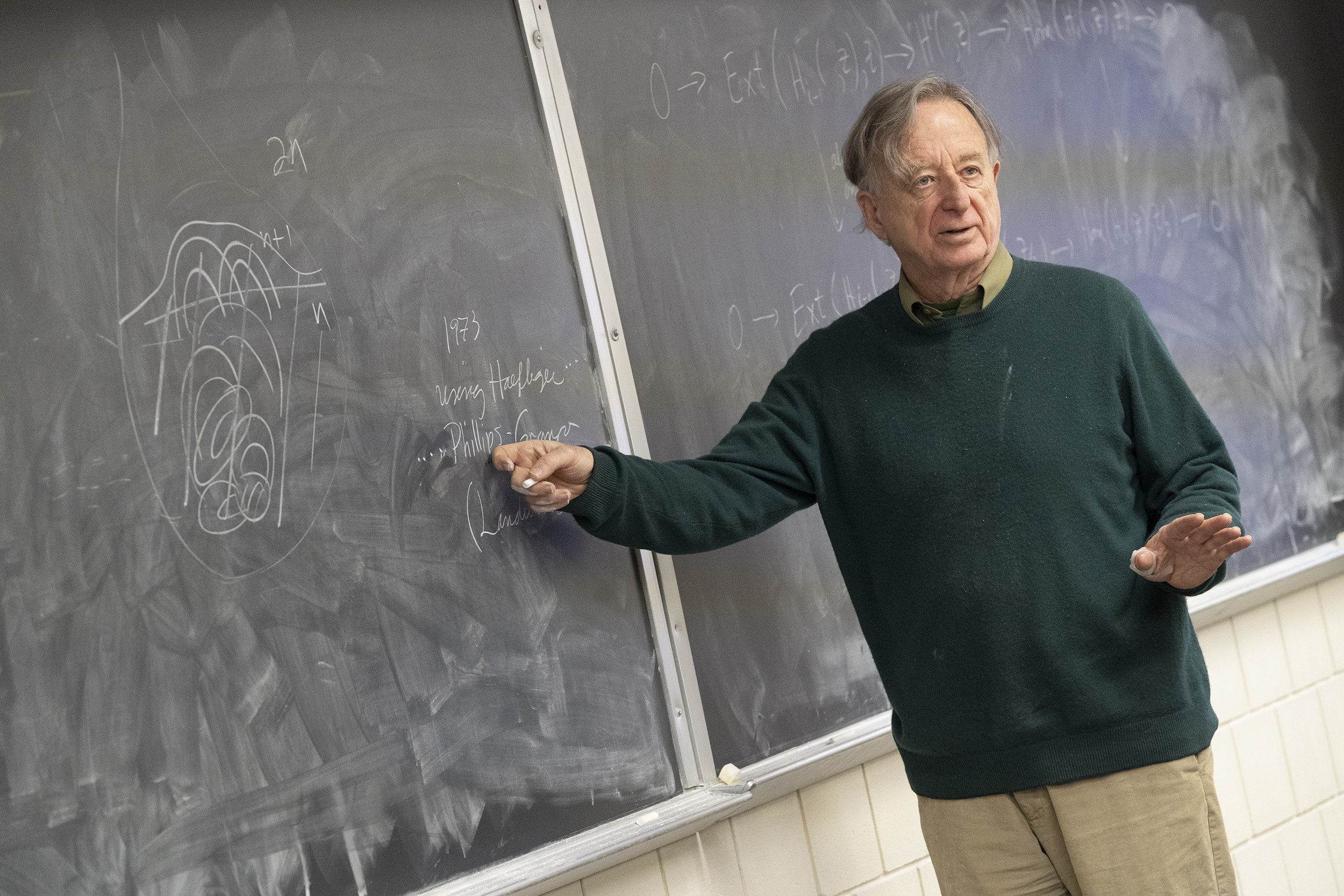
Dennis Sullivan lectures at the blackboard at Stony Brook University in New York
Dennis Sullivan lectures at the blackboard at Stony Brook University in New York (Image credit: John Griffin/Stony Brook University/ Abel Prize)

American mathematician Dennis Sullivan has been awarded the 2022 Abel Prize, one of the most prestigious awards in math, for his contributions to the fields of topology and dynamical systems.

According to a statement from The Norwegian Academy of Science and Letters (DNVA), which distributes the award each year along with a prize that's equivalent to about $864,000 ($7.5 million Norwegian kroner), Sullivan has been recognized "for his groundbreaking contributions to topology in its broadest sense, and in particular its algebraic, geometric and dynamical aspects."

Topology is the study of properties of objects and spaces that do not change when they are deformed. The field is sometimes called "rubber-sheet geometry," because objects can be stretched into different shapes like rubber but cannot be broken, according to the University of Waterloo in Ontario. For example, a square can be deformed into a circle without breaking, but a doughnut shape cannot. Thus, a square is topologically equivalent to a circle, but a doughnut isn't.

Sullivan, now a professor of mathematics at Stony Brook University in New York, was born in Port Huron, Michigan, on Feb. 12, 1941. He began studying topology as a graduate student at Princeton University in the early 1960s. His 1966 doctoral thesis, called "Triangulating Homotopy Equivalences," helped revolutionize the study of manifolds, spaces that look flat when viewed from any point on their surface but have a more complicated overall structure (like the surface of a sphere), according to the DNVA.

"During this time, he gradually changed the way mathematicians thought about algebraic and geometric topology, introducing new ideas and building a new vocabulary," according to the DNVA. "In 1970, he wrote a set of unpublished notes that were widely circulated and considered hugely influential, directly impacting the classification of smooth manifolds and central problems in algebraic topology." (These so-called MIT notes were finally published in 2006.)

By the late 1970s, Sullivan began investigating problems in dynamical systems, which is the study of a point moving through a geometrical space and a fundamental part of chaos theory. His work united dynamical systems and algebraic topology in ways that had never been done. In 1985, Sullivan proved a 60-year-old conjecture that points moving through complex dynamical systems in fractal patterns eventually return to their starting point rather than wandering about endlessly, according to Quanta Magazine.

"Dennis P. Sullivan has repeatedly changed the landscape of topology by introducing new concepts, proving landmark theorems, answering old conjectures and formulating new problems that have driven the field forwards," Hans Munthe-Kaas, chair of the Abel Committee, said in the DNVA statement. "I'm not sure he sees the boundaries between different areas of mathematics the same as other people see it."

For more, read a full biography of Sullivan and his career highlights, courtesy of the DNVA.

Originally published on Live Science.

Brandon Specktor
Brandon Specktor
Editor

Brandon is the space / physics editor at Live Science. With more than 20 years of editorial experience, his writing has appeared in The Washington Post, Reader's Digest, CBS.com, the Richard Dawkins Foundation website and other outlets. He holds a bachelor's degree in creative writing from the University of Arizona, with minors in journalism and media arts. His interests include black holes, asteroids and comets, and the search for extraterrestrial life.