12 numbers that are cooler than pi
To celebrate Pi Day, we asked several mathematicians to tell us their favorite non-pi numbers. Here are some of their answers.
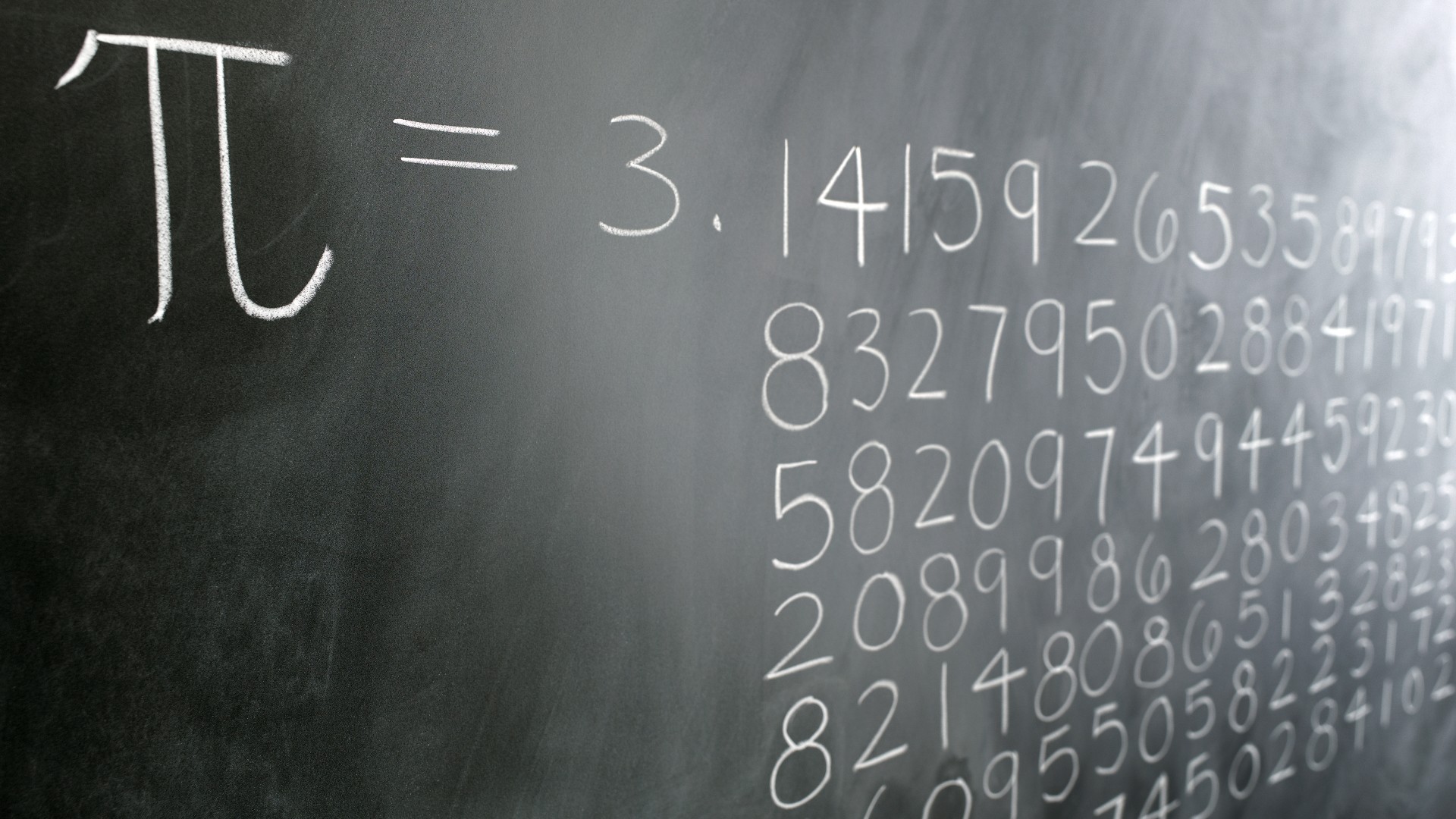
Here at Live Science, we love numbers. And on Pi Day — March 14, or 3/14 — we love to celebrate the world's most famous irrational number, pi, whose first 10 digits are 3.141592653.
As the ratio of a circle's circumference to its diameter, pi is not just irrational, meaning it can't be written as a simple fraction. It is also transcendental, meaning it's not the root, or solution, to any polynomial equation, such as x+2X^2+3 = 0.
Pi may be one of the best-known numbers, but for people who are paid to think about numbers all day long, the circle constant can be a bit of a bore. We asked several mathematicians to tell us their favorite non-pi numbers. Here are some of their answers.
Tau

You know what's cooler than one pie? … Two pies. In other words, two times pi, or the number "tau," which is roughly 6.28.
"Using tau makes every formula clearer and more logical than using pi," said John Baez, a mathematician at the University of California, Riverside. "Our focus on pi rather than 2pi is a historical accident."
Tau is what shows up in the most important formulas, he said.
While pi relates a circle's circumference to its diameter, tau relates a circle's circumference to its radius — and many mathematicians argue that this relationship is much more important. Tau also makes seemingly unrelated equations nicely symmetrical, such as the one for a circle's area and an equation describing kinetic and elastic energy.
But tau will not be forgotten on Pi Day! As per tradition, the Massachusetts Institute of Technology will send out decisions at 6:28 p.m. today. A few months from now, on June 28, it will be Tau Day.
Natural log

The base of natural logarithms — written as "e" for its namesake, the 18th-century Swiss mathematician Leonhard Euler — may not be as famous as pi, but it also has its own holiday. So, while 3.14 is celebrated on March 14, natural log base — the irrational number beginning with 2.718 — is lionized on Feb. 7.
The base of natural logarithms is most often used in equations involving logarithms, exponential growth and complex numbers.
"[It] has the wonderful definition as being the one number for which the exponential function y = e^x has a slope equal to its value at every point," Keith Devlin, emeritus professor and former director of the Stanford University Mathematics Outreach Project in the Graduate School of Education, told Live Science. In other words, if the value of a function is, say, 7.5 at a certain point, then its slope, or derivative, at that point is also 7.5. And, "like pi, it comes up all the time in mathematics, physics and engineering," Devlin said.
Imaginary number i
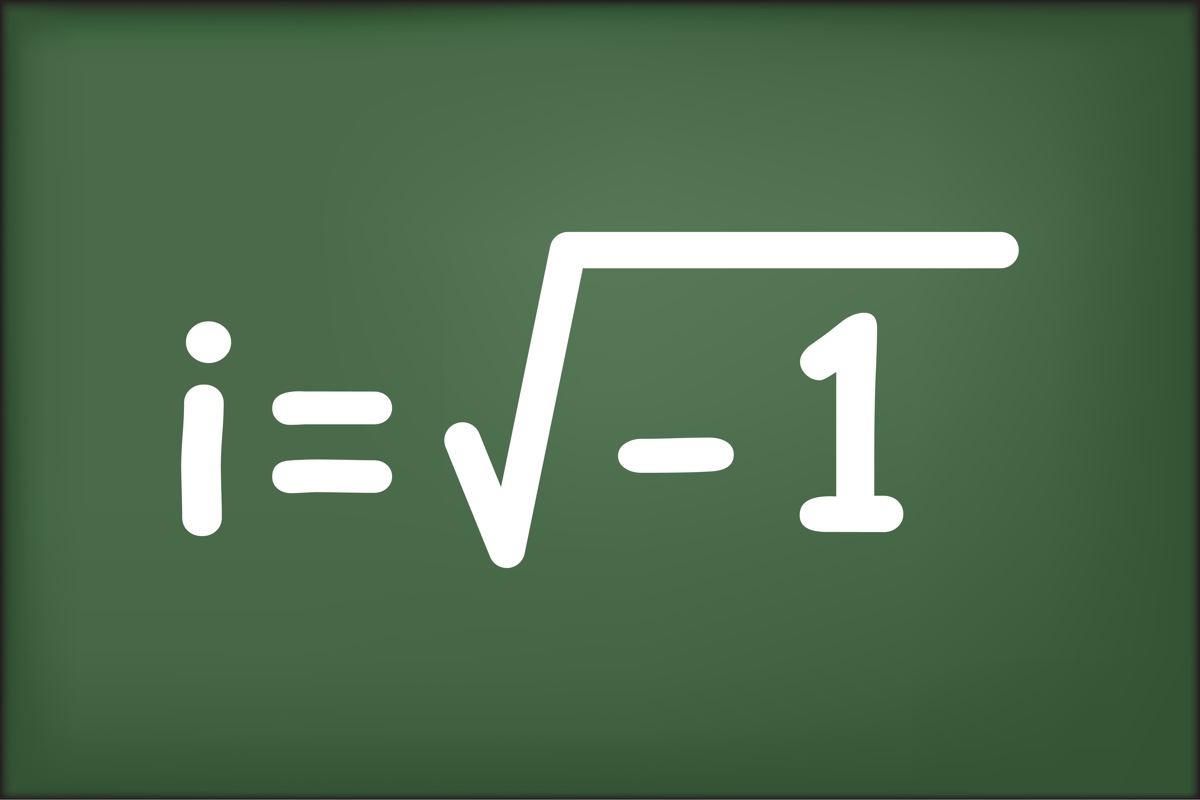
Take the "p" out of "pi," and what do you get? That's right, the number i. No, that's not really how it works, but i is a pretty cool number. It's the square root of -1, which means it's a rule breaker, as you're not supposed to take the square root of a negative number.
"Yet, if we break that rule, we get to invent the imaginary numbers, and so the complex numbers, which are both beautiful and useful," Eugenia Cheng, a mathematician at the School of the Art Institute of Chicago, told Live Science in an email. (Complex numbers can be expressed as the sum of both real and imaginary parts.)
The imaginary number i is an exceptionally weird number because -1 has two square roots: i and -i, Cheng said. "But we can't tell which one is which!" Mathematicians have to just pick one square root and call it i and the other -i.
"It's weird and wonderful," Cheng said.
i to the power i

Believe it or not, there are ways to make i even weirder. For example, you can raise i to the power of i — in other words, take the square root of -1 raised to the square root of -1 power.
"At a glance, this looks like the most imaginary number possible — an imaginary number raised to an imaginary power," David Richeson, a professor of mathematics at Dickinson College in Pennsylvania and author of the book "Tales of Impossibility: The 2,000-Year Quest to Solve the Mathematical Problems of Antiquity" (Princeton University Press, 2019), told Live Science. "But, in fact, as Leonhard Euler wrote in a 1746 letter, it is a real number!"
Finding the value of i to the i power involves rearranging Euler's identity, a formula relating the irrational number e, the imaginary number i, and the sine and cosine of a given angle. When you solve the formula for a 90-degree angle (which can be expressed as pi over 2), you can simplify the equation to show that i to the power of i equals e raised to the power of negative pi over 2.
It sounds confusing (here's the full calculation, if you dare to read it), but the result equals roughly 0.207 — a very real number. At least, in the case of a 90-degree angle.
"As Euler pointed out, i to the i power does not have a single value," Richeson said, but rather takes on "infinitely many" values depending on the angle you're solving for. (Because of this, it's unlikely we'll ever celebrate an "i to the power of i day.")
Belphegor's prime number

Belphegor's prime number is a palindromic prime number with a 666 hiding between 13 zeros and a 1 on each side. The ominous number can be abbreviated as 1 0(13) 666 0(13) 1, where the (13) denotes the number of zeros between the 1 and 666.
Although he didn't "discover" the number, scientist and author Cliff Pickover made the sinister-looking number famous when he named it after Belphegor (or Beelphegor), one of the seven demon princes of hell in the Bible.
The number apparently even has its own devilish symbol, which looks like an upside-down symbol for pi. According to Pickover's website, the symbol is derived from a glyph in the mysterious Voynich manuscript, an early-15th-century compilation of illustrations and text that no one seems to understand.
2^{aleph_0}

Harvard mathematician W. Hugh Woodin has devoted many years of research to infinite numbers. It's no surprise, then, that his favorite number is an infinite one: 2^{aleph_0}, or 2 raised to the power of aleph-naught, also called aleph-null. Aleph numbers are used to describe the sizes of infinite sets, where a set is any collection of distinct objects in mathematics. (So, for example, the numbers 2, 4 and 6 can form a set of size 3.)
As for why Woodin chose the number, he said, "Realizing that 2^{aleph_0} is not \aleph_0 (i.e., Cantor's theorem) is the realization that there are different sizes of infinite. So that makes the conception of 2^{\aleph_0} rather special."
In other words, there's always something bigger: Infinite cardinal numbers are infinite, so there is no such thing as the "largest cardinal number."
Apéry's constant

Harvard mathematician Oliver Knill told Live Science his favorite number is the Apéry's constant (zeta(3)), "because there is still some mystery associated with it." In 1979, French mathematician Roger Apéry proved that a value that would come to be known as Apéry's constant is an irrational number. (It begins with 1.2020569 and continues infinitely.) The constant is also written as zeta(3), where zeta(3) is the Riemann zeta function when you plug in the number 3.
One of the biggest outstanding problems in math, the Riemann hypothesis, makes a prediction about when the Riemann zeta function equals zero and, if proven, would allow mathematicians to better predict how the prime numbers are distributed.
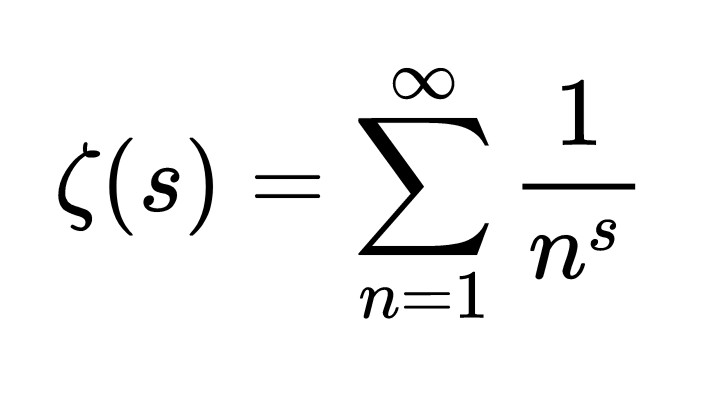
Of the Riemann hypothesis, renowned 20th-century mathematician David Hilbert once said, "If I were to awaken after having slept for a thousand years, my first question would be, 'Has the Riemann hypothesis been proven?'"
So what's so cool about this constant? It turns out that Apéry's constant shows up in fascinating places in physics, including in equations governing the electron's magnetism and orientation to its angular momentum.
The number 1

Ed Letzter, a mathematician at Temple University in Philadelphia (and father of former Live Science staff writer Rafi Letzter), had a practical answer:
"I suppose this is a boring answer, but I'd have to choose 1 as my favorite, both as a number and in its different roles in so many different more abstract contexts," he told Live Science.
One is the only number by which all other numbers divide into integers. It's the only number divisible by exactly one positive integer (itself, 1). It's the only positive integer that's neither prime nor composite.
In both math and engineering, values are often represented as between 0 and 1: "100%" is just a fancy way of saying 1. It's whole and complete.
And, of course, throughout the sciences, 1 is used to represent basic units. A single proton is said to have a charge of +1. In binary logic, 1 means yes. It's the atomic number of the lightest element, and it's the dimension of a straight line.
Euler's identity

Euler's identity, which is actually an equation, is a real mathematical jewel, at least as described by the late physicist Richard Feynman. It has also been compared to a Shakespearean sonnet.
In a nutshell, Euler's identity ties together a number of mathematical constants: pi, natural log e and the imaginary unit i.
"[It] connects these three constants with the additive identity 0 and the multiplicative identity of elementary arithmetic: e^{i*Pi} + 1 = 0," Devlin said.
The number 0

If we're already talking about how awesome 1 is, then why not throw in the even weirder and cooler number 0? For most of written human history, the concept of zero wasn't all that important. Clay tablets from ancient Babylonian times didn't always distinguish between numbers like 216 and 2106, according to the University of St. Andrews in Scotland.
The ancient Greeks began to develop the idea of using zero as an empty place indicator to distinguish numbers of different magnitudes, but it wasn't until roughly the seventh century that Indian mathematicians, like Brahmagupta, began describing the modern idea of zero. Brahmagupta wrote that any number multiplied by zero is zero, but he struggled with division, saying that a number, n, divided by zero just comes out as n/0, rather than the modern answer, which is that the result is undefined. (The Maya had also independently derived the concept of zero by A.D. 665.)
Zero is extremely useful, but it is a very tricky concept for many people to wrap their heads around. We have examples such as 1 horse or 3 chickens in our day-to-day lives, but using a number to represent nothing is a larger conceptual leap. "Zero is in the mind but not in the sensory world," the late Robert Kaplan, a Harvard math professor, told Vox (Kaplan died in 2021). Still, without 0 (and 1), we wouldn't be able to represent all of the digital binary code that makes our contemporary world run. (Data on computers is represented by strings of 0s and 1s.)
The square root of 2

Perhaps the most dangerous number ever conceived, the square root of 2 supposedly led to the first mathematical murder in history. The Greek mathematician Hippasus of Metapontum is credited with discovering it in the fifth century B.C., according to the University of Cambridge. While working on a separate problem, Hippasus is said to have stumbled on the fact that an isosceles right triangle whose two base sides are 1 unit in length will have a hypotenuse that is √2, which is an irrational number.
According to legend, Hippasus' contemporaries, members of the quasi-religious order known as the Pythagoreans, threw him into the sea after hearing about his great discovery. That's because the Pythagoreans believed that "all is number" and the universe only contained whole numbers and their ratios. Irrational numbers like √2 (and pi), which can't be expressed as a ratio of whole numbers and go on forever after the decimal place, were seen as an abomination.
These days, we're a little calmer about √2, often calling it Pythagoras' constant. It starts off as 1.4142135623 … (and, of course, goes on forever). ) Pythagoras' constant has all sorts of uses. Besides proving the existence of irrational numbers, it is used by the International Organization for Standardization (ISO) to define the A paper size. The 216 definition of the A paper states that the sheet's length divided by its width should be 1.4142. This means that a piece of A1 paper divided in half by width will yield two A2 pieces of paper. Divide an A2 in half again, and it will produce two A3 pieces of paper, and so on.
Slice of pi

Sometimes, the number cooler than pi is...a truncated version of pi. At least, that's the case for NASA and scientists at the Jet Propulsion Laboratory (JPL) in California. For interplanetary navigation, JPL uses the number 3.141592653589793, according to JPL's Chief Engineer for Mission Operations and Science, Marc Rayman . At that level of accuracy, Rayman said, NASA can get everything it builds wherever it needs to go.
To see why, it's helpful to do some number-crunching. The most distant spacecraft from Earth is the Voyager 1 spacecraft, which is more than 14.6 billion miles (23.5 billion kilometers) distant from us. At this distance, you can calculate a circumference of a circle that is roughly 94 billion miles (more than 150 billion km) around, yet adding extra decimal places to pi only shaves off a half-inch (1.2 centimeters) of error from the calculation, Rayman said.
Even if scientists wanted to calculate the radius of a circle the size of the known universe to the accuracy of a width of a hydrogen atom, it would only need 37 digits after the decimal point to reach that accuracy, Rayman said.
So what's cooler than pi? A slice of pi.
Get the world’s most fascinating discoveries delivered straight to your inbox.
- Adam MannLive Science Contributor

