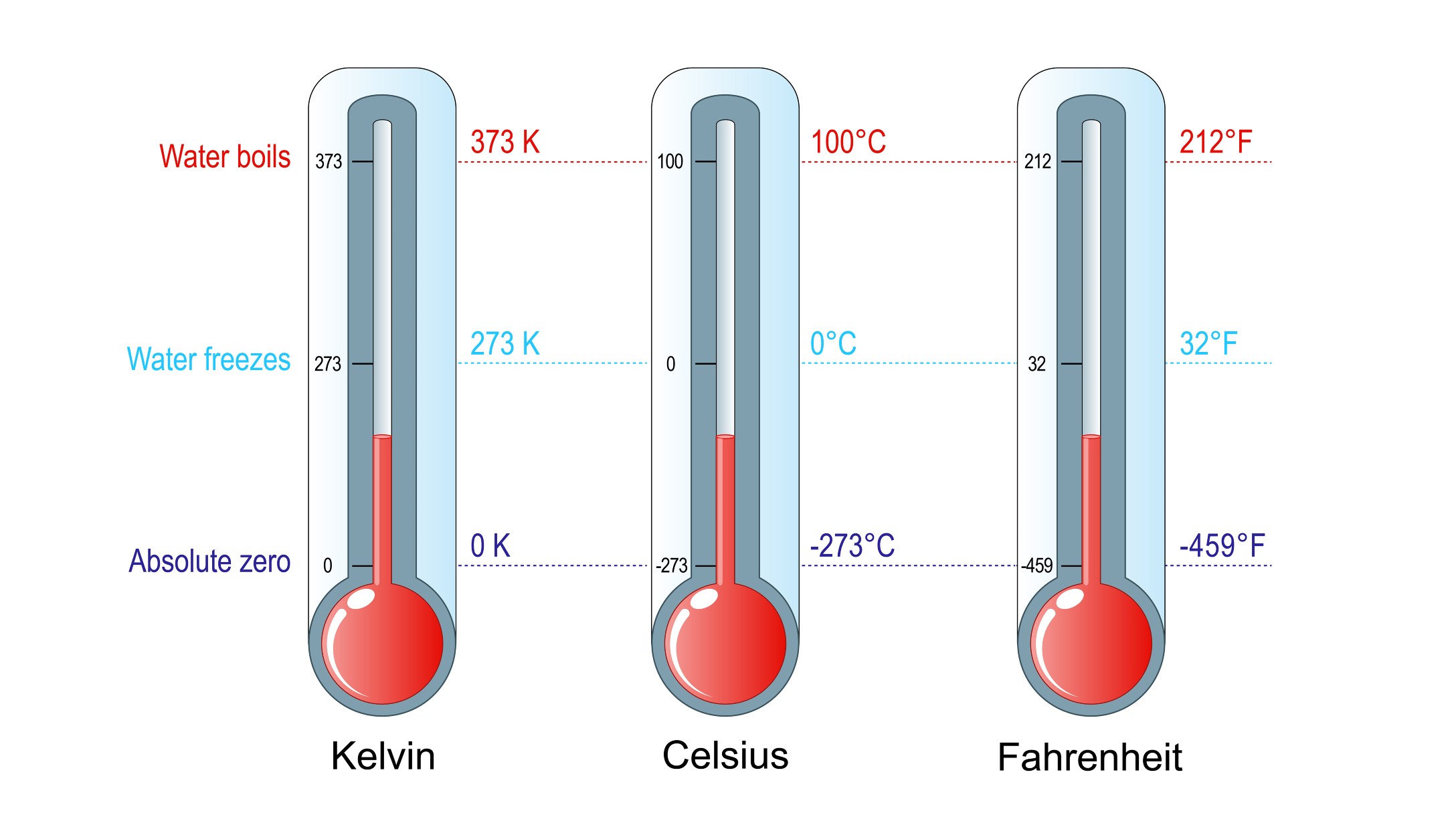
The third law of thermodynamics is concerned with behavior of systems as the temperature approaches absolute zero. It relates heat and entropy at this ultimate lowest temperature for crystals, which refer to any solid material made up of atoms arranged in a definite, symmetrical pattern, according to Britannica. The third law of thermodynamics states, "the entropy of a perfect crystal is zero when the temperature of the crystal is equal to absolute zero (0 K)." According to Purdue University, "the crystal must be perfect, or else there will be some inherent disorder. It also must be at 0 K; otherwise there will be thermal motion within the crystal, which leads to disorder."
Siabal Mitra, a professor of physics at Missouri State University, provides another implication of this law.
"One version of the third law states that it would require an infinite number of steps to reach absolute zero, which means you will never get there," Mitra told Live Science. If you could get to absolute zero, it would violate the second law, because if you had a heat sink at absolute zero, then you could build a machine that was 100% efficient."
In theory, it would be possible to grow a perfect crystal in which all of the lattice spaces are occupied by identical atoms. However, it is generally believed that it is impossible to achieve a temperature of absolute zero. Therefore, all matter contains at least some entropy owing to the presence of some heat energy.
History of the third law of thermodynamics
The third law of thermodynamics was first formulated by German chemist and physicist Walther Nernst in 1906, according to Britannica. In his book, "A Survey of Thermodynamics" (American Institute of Physics, 1994), Martin Bailyn quotes Nernst's statement of the third law as, "It is impossible for any procedure to lead to the isotherm T = 0 in a finite number of steps." This essentially establishes a temperature of absolute zero as being unattainable in somewhat the same way as the speed of light c in a vacuum can never be exceeded. Theory states and experiments have shown that no matter how fast something is moving, it can always be made to go faster, but it can never reach the speed of light, according to Morningside University. Similarly, no matter how cold a system is, it can always be made colder, but it can never reach absolute zero.
In her book, "The Story of Physics" (Arcturus, 2012), Anne Rooney wrote, "The third law of thermodynamics requires the concept of a minimum temperature below which no temperature can ever fall — known as absolute zero." She continued, "Robert Boyle first discussed the concept of a minimum possible temperature in 1665, in 'New Experiments and Observations Touching Cold' [Crook Publishing], in which he referred to the idea as primum frigidum."
Absolute zero is believed to have been first calculated with reasonable precision in 1779 by Johann Heinrich Lambert, according to Jaime Wisniak of Ben-Gurion University of the Negev in Israel. Lambert based this calculation on the linear relationship between the pressure and temperature of a gas. When a gas is heated in a confined space, its pressure increases. This is because the temperature of a gas is a measure of the average speed of the molecules in the gas. The hotter it gets, the faster the molecules move, and the greater the pressure they exert when they collide with the walls of the container. It was reasonable for Lambert to assume that if the temperature of the gas could be brought to absolute zero, the motion of the gas molecules could be brought to a complete stop so they could no longer exert any pressure on the walls of the chamber.
If one were to plot the temperature-pressure relationship of the gas on a graph with temperature on the x (horizontal) axis and pressure on the y (vertical) axis, the points would form an upward-sloping straight line, indicating a linear relationship between temperature and pressure, according to Florida State University. It should be rather simple, then, to extend the line backward and read the temperature where the line crosses the x axis, i.e., where y = 0, indicating zero pressure. Using this technique, Lambert calculated absolute zero to be minus 270 degrees Celsius (minus 454 Fahrenheit), which was remarkably close to the modern accepted value of minus 273.15 C (minus 459.67 F), according to Britannica.
The Kelvin temperature scale
The person most associated with the concept of absolute zero is William Thomson, 1st Baron Kelvin. The temperature unit bearing his name, the kelvin (K), is the one most commonly used by scientists worldwide. Temperature increments in the Kelvin scale are the same size as in the Celsius scale, but because it starts at absolute zero, rather than the freezing point of water, it can be used directly in mathematical calculations, particularly in multiplication and division. For example, 100 K actually is twice as hot as 50 K, according to the University of Texas. A sample of confined gas at 100 K also contains twice as much thermal energy, and it has twice the pressure as it would have at 50 K. Such calculations cannot be done using the Celsius or Fahrenheit scales, i.e., 100 C is not twice as hot as 50 C, nor is 100 F twice as hot as 50 F.
Implications of the third law
Because a temperature of absolute zero is physically unattainable, the third law may be restated to apply to the real world as: The entropy of a perfect crystal approaches zero as its temperature approaches absolute zero. We can extrapolate from experimental data that the entropy of a perfect crystal reaches zero at absolute zero, but we can never demonstrate this empirically.
"There's a field of ultra-low-temperature research, and every time you turn around there's a new record low. These days, nanokelvin (nK = 10^−9 K) temperatures are reasonably easy to achieve, and everyone's now working on picokelvins (pK = 10^−12 K)," said David McKee, a professor of physics at Missouri Southern State University.
As of this writing, the record-low temperature was achieved in 2021 by a team at the Center for Applied Space Technology and Microgravity (ZARM) at the University of Bremen in Germany. They trapped a cloud of around 100,000 rubidium atoms in a magnetic field inside a vacuum chamber and tossed the chamber down a drop tower to let the atoms float uninhibited by gravity and slow their molecular motion. The cloud reached a record 38 picokelvins, or 38 trillionths of a Kelvin.
While a temperature of absolute zero does not exist in nature, and scientists cannot achieve it in the laboratory, the concept of absolute zero is critical for calculations involving temperature and entropy. Many measurements imply a relationship to some starting point. When someone provides a distance, they have to ask, distance from what? When they give a time, they have to ask, time since when? Defining the zero value on the temperature scale gives meaning to positive values on that scale. When a temperature is stated as 100 K, it means that the temperature is 100 K above absolute zero, which is twice as far above absolute zero as 50 K and half as far as 200 K.
On first reading, the third law seems rather simple and obvious. However, it serves as the final period at the end of a long and consequential story that fully describes the nature of heat and thermal energy.
This article was updated on Feb. 2, 2022 by Live Science contributor Ashley Hamer.
Additional resources
- The University of Calgary's Energy Education website explains the concept of absolute zero.
- In this video from StarTalk, Neil deGrasse Tyson explains why you can't reach absolute zero.
- Rensselaer Polytechnic Institute has another explanation of the third law of thermodynamics, complete with three different formulations of the law.
Bibliography
Purdue University, "Entropy and the 2nd & 3rd Laws of Thermodynamics." http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch21/entropy.php
The Nobel Prize, "Walther Nernst: Biographical." 1966. https://www.nobelprize.org/prizes/chemistry/1920/nernst/biographical/
Martin Bailyn, "A Survey of Thermodynamics," American Institute of Physics, 1994
Morningside University, "The Limit of Speed." https://webs.morningside.edu/slaven/Physics/relativity/relativity10.html
Anne Rooney, "The Story of Physics," Arcturus, 2012
Robert Boyle, "New Experiments and Observations Touching Cold," Crook, 1665
Jaime Wisniak, "Development of the Concept of Absolute Zero Temperature," Educación Química, January 2005 https://www.researchgate.net/publication/236235474_Development_of_the_Concept_of_Absolute_Zero_Temperature
Illinois State University, "MAT 312: Probability and Statistics for Middle School Teachers," https://math.illinoisstate.edu/day/courses/old/312/notes/twovar/twovar02.html
Florida State University, "Gas Laws." https://www.chem.fsu.edu/chemlab/chm1045/gas_laws.html
Britannica, "Absolute zero," April 9, 2021. https://www.britannica.com/science/absolute-zero
The University of Texas Health Science Center at Houston, "Biostatistics for the Clinician." https://www.uth.tmc.edu/uth_orgs/educ_dev/oser/L1_2.HTM
University of Bremen, "Extremely Long and Incredibly Cold," August 27, 2021. https://www.zarm.uni-bremen.de/en/press/single-view/article/extremely-long-and-incredibly-cold.html
