This Biologist Cracked a Problem That's Stumped Mathematicians for 68 Years

An amateur mathematician just partially solved a problem that has vexed mathematicians since 1950.

Aubrey de Grey — a biologist better known for trying to radically extend human life and for predicting that the first person to live to be 1,000 years old has already been born — has published a paper on the preprint server arXiv that narrows down the answer to the 68-year-old Hadwiger-Nelson problem. Mathematicians had known for years that the answer to this question (which we'll get to in a second) was either 4, 5, 6 or 7. De Grey, in his paper, showed that it definitely isn't 4. That leaves just 5, 6 or 7. [The 9 Most Massive Numbers in Existence]

Now that you have de Grey's answer, here's the question:

Take a canvas and draw a bunch of points (called vertices) on it. If any points are a distance 1 unit apart from each other, draw a line between them. Mathematicians don't care if the "unit" is an inch or a mile. It doesn't matter, as long as it's the same between all connected vertices. (Those lines connecting the points are called "edges.") Mathematicians call this a unit distance graph. What you end up with will look something like this:

(Image credit: Aubrey de Gray/arXiv/CC by 4.0)

Now it's time to go to the store and buy paint to color in all the points.

Now ask yourself: What's the minimum number of paint colors I need to color in any graph in a way that no two points that share an edge are the same color?

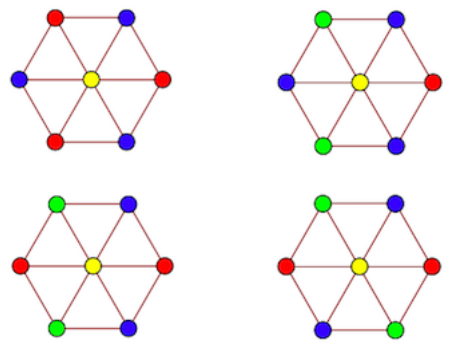
It's easy to come up with a unit distance graph that can't be colored with just three colors. Here's a good example:

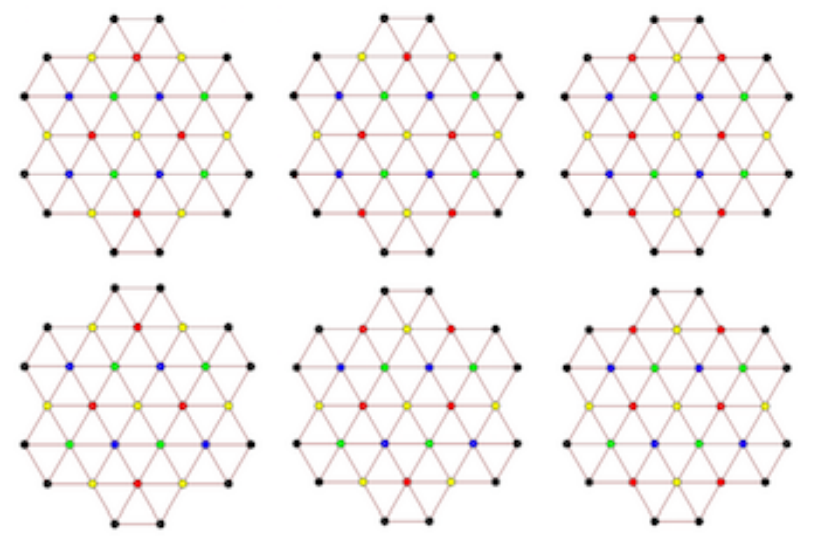
This graph cannot be colored with just three colors, but four will do the trick. Black dots denote that the pattern can be repeated on an infinite plane. (Image credit: Aubrey de Gray/arXiv/CC by 4.0)

But coming up with a unit distance graph that can't be colored in with four colors is a lot more difficult. Computers can't do it on their own. No full-time mathematicians managed it for 68 years, until de Grey came up with this monstrosity:

De Grey's graph has 1,581 vertices on it. And they're arranged in such a way that you couldn't paint it just right with four colors of paint. At least five are necessary to make it work.

But that doesn't mean five is the absolute minimum. Mathematicians know that it's possible that a graph will come along requiring six colors of paint, or even seven. (Back in 1950, the mathematician John Isbell came up with a strategy involving seven colors for solving any graph.)

The absolute minimum needed is still a mystery. But thanks to de Grey, we know it's more than four.

Original article on Live Science.

Rafi joined Live Science in 2017. He has a bachelor's degree in journalism from Northwestern University’s Medill School of journalism. You can find his past science reporting at Inverse, Business Insider and Popular Science, and his past photojournalism on the Flash90 wire service and in the pages of The Courier Post of southern New Jersey.