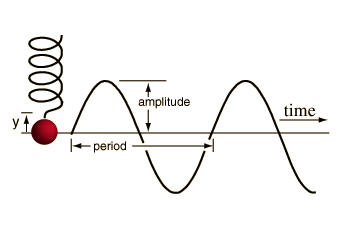
What Is Simple Harmonic Motion?

When a musician strums a guitar, the vibration of the strings creates sound waves that human ears hear as music. When a guitar string is plucked, it moves a certain distance, depending on how hard the guitar player strums. The string returns to its starting point and travels nearly the same distance in the opposite direction. The vibrational energy of the string is dissipated in the form of sound. This causes the distance the string moves, or the amplitude of the vibrations, to decrease gradually. The volume of the sound fades until the string eventually falls silent.
The guitar string is an example of simple harmonic motion, or SHM. SHM can be seen throughout nature. It describes the vibration of atoms, the variability of giant stars, and countless other systems from musical instruments to swaying skyscrapers.
Princeton University's WordNet defines simple harmonic motion as “periodic motion in which the restoring force is proportional to the displacement.” Periodic means that the motion repeats at a constant, predictable rate. The part about the restoring force being proportional to the displacement simply means the farther you push something, the harder it pushes back.
SHM also describes the motion of a ball hanging from a spring. The ball is subject to a linear elastic restoring force, according to Georgia State University's HyperPhysics website. Drawn out on a graph, the up-and-down motion of the ball over time can be illustrated as a smooth, repetitive oscillation, or sinusoidal wave. The shape of the wave can be calculated using Hooke's Law.
Robert Hooke was a British scientist, mathematician and architect who was interested in many aspects of science and technology, from astronomy to microbiology. Studying objects under a magnifying glass, he was the first to use the word "cell" to describe the components of plant tissues, according to the Physics Hypertextbook. He also studied clocks and timekeeping, and in 1675 developed a theory of elasticity or springiness as a way to regulate pendulum clocks. In short, the theory says, "Extension is directly proportional to force."
Mathematically, Hooke’s Law is expressed as F = −kx, where F is the force, x is the change in length from the spring’s relaxed or original length, and k is the characteristic spring constant that specifies the amount of force required to stretch or compress the spring a certain distance. The minus sign indicates that the restoring force is in the opposite direction of the displacement.
Circular motion
There is a close connection between circular motion and simple harmonic motion, according to Boston University. Consider a point on the rim of a disk as it rotates counterclockwise at a constant rate around a horizontal axis. If we plot only the vertical position of the point as the disk turns, it produces a sinusoidal graph. This is exactly the same graph as we get if we plot the position of a mass on a spring bouncing up and down in simple harmonic motion as a function of time.
Get the world’s most fascinating discoveries delivered straight to your inbox.
Pendulums
Simple pendulums behave much like harmonic oscillators such as springs. However, the period of a pendulum is determined not by its mass but by its length. Another significant difference is that in the case of a pendulum, the restoring force is provided not by a spring but by gravity. Since gravity is pulling the pendulum vertically downward and not back along the arc in the opposite direction of its motion, the restoring force is a somewhat complex trigonometric function. Nevertheless, pendulums closely approximate simple harmonic motion provided they don’t swing more than a few degrees from their resting point.
Damped harmonic motion
All mechanical systems are subject to damping forces, which cause the amplitude of the motion to decrease over time. These forces can include frictional forces between moving parts, air resistance or internal forces such as those in springs that tend to dissipate energy as heat.
In simple harmonic motion, the damping force is generally proportional to the velocity of the oscillating mass, according to the State University of New York Stony Brook. This force will eventually bring an oscillating system to a halt, and if it is great enough, it can actually stop oscillations before they can start.
A weight on a spring bouncing in air will continue bouncing for quite a long time, but not forever. Air resistance and internal resistance in the metal spring will eventually dissipate the kinetic energy of the system and bring it to a stop. However, if the weight were suspended in a pot of cold molasses, and the spring is stretched and released, the weight might only return slowly to its rest position without bouncing above it even once. We consider the weight bouncing in air to be underdamped, and the weight moving slowly through molasses and never bouncing even once to be overdamped. If the system is exactly on the cusp between these two conditions, it is said to be critically damped.
“We know that in reality, a spring won't oscillate forever. Frictional forces will diminish the amplitude of oscillation until eventually the system is at rest,” according to the University of California Santa Cruz. The amplitude of an underdamped oscillator undergoes an exponential decay, meaning that after a certain time, the amplitude of the oscillations will decrease by half, and after that same time period, it will decrease again by half. One familiar example of this is the decaying sound of a bell.
In many cases, damping is desired to prevent uncontrolled bouncing. Perhaps the most familiar example of this is an automobile suspension system. The wheels are mounted on springs so they can move up and down in response to bumps and dips in the road while the body of the car remains relatively level. However, without damping, the car would begin to bounce up and down uncontrollably. To prevent this, cars have shock absorbers to damp the movement of the springs by adding a frictional force to the suspension system.
Driven harmonic motion
When it is desirable for harmonic motion to persist, damping is a problem that must be overcome with a driving force. Consider the pendulum in a grandfather clock. At its farthest point in each direction, an escapement mechanism, powered by the gravitational energy of a slowly descending weight, gives the pendulum a tiny nudge that is sufficient to overcome the damping effect of mechanical friction and air resistance and maintain the pendulum’s motion.
One manifestation of driven harmonic motion is coupled resonance, or sympathetic vibration. This is a vibration that is produced in one body by the vibrations of exactly the same period in a neighboring body. One familiar example of this is a playground swing set. If it has two swings of the same length, swinging on one swing can cause the other one to start moving. The reason for this is that the first swing causes the supporting cross bar to move forward and back slightly with each cycle. Although this motion is usually small, because swings are the same length, they will have the same resonant frequency, so the driving force provided by the tiny motions of the cross bar become amplified, causing the second swing to move noticeably. Another example of a harmonic oscillator being driven at its resonant frequency is how an electric guitar can sustain a note indefinitely by allowing feedback of the amplified sound to drive the continued vibration of the string.
Sometimes, though, harmonic motion under a driving force can be harmful or even disastrous. If this force is applied at the natural or resonant frequency of the oscillating system at a rate that is greater than damping forces can dissipate the energy, “…relatively small driving forces can build up to large-amplitude oscillations, just because energy is continually being injected into the system at just the right frequency,” according to Boston University. This means that if an underdamped system is driven by external forces at its resonant frequency, the amplitude of the motion can increase until the system fails. One of the most dramatic examples of this is the 1940 Tacoma Narrows Bridge collapse. Strong sustained winds drove oscillations of the bridge deck that increased in amplitude until it broke apart. Another example of harmonic motion being driven to the point of failure is how singer can shatter a wine glass by loudly singing a note at its resonant frequency.
Harmonic motion in real life is rarely simple. When we look at real macroscopic oscillating systems, there can be any number confounding variables, such as fluctuations in temperature and air pressure or wear and tear on mechanical parts, which can affect the amplitude and period of the motion. However, by assuming that mechanical systems are in simple harmonic motion, we can often make suitably accurate approximations of how these systems behave.
Additional resources