How much does Earth weigh?
Earth's mass took hundreds of years to estimate, and even now, experts don't agree on the exact number.

Our planet holds everything from hard rocks and minerals to millions of species of living things, and is covered in countless natural and human-made structures.
So how much does all of that weigh? There's no single answer to that question. Just like humans weigh much less on the moon than we do at home, Earth doesn't have just one weight. Earth's weight depends on the gravitational force pulling on it, which means it could weigh trillions of pounds or nothing at all.
What scientists have spent centuries determining, however, is Earth's mass, which is its resistance to movement against an applied force. According to NASA, Earth's mass is 5.9722×1024 kilograms, or around 13.1 septillion pounds. This equates to around 13 quadrillion of Egypt's pyramid of Khafre, which itself weighs around 10 billion pounds (4.8 billion kilograms). The Earth's mass fluctuates slightly due to the addition of space dust and gases leaking out of our atmosphere, but these tiny changes won't affect Earth for billions of years.
Physicists around the world still don't agree on the decimals, though, and getting to that grand total has been no easy task. Because it's impossible to put Earth on a scale, scientists had to triangulate its mass using other measurable objects.
Related: How do we know how old Earth is?
The first component was Isaac Newton's law of universal gravitation, Stephan Schlamminger, a metrologist at the U.S. National Institute of Standards and Technology, told Live Science. Everything that has mass also has a gravitational force, meaning any two objects will always have some force between them.
Newton's law of universal gravitation states that the gravitational force between two objects (F) can be determined by multiplying the respective masses of the objects (m₁ and m₂), dividing by the distance between the centers of the objects squared (r²), and then multiplying that number by the gravitational constant (G), otherwise known as the intrinsic strength of gravity, or F=G((m₁*m₂)/r²).
Get the world’s most fascinating discoveries delivered straight to your inbox.
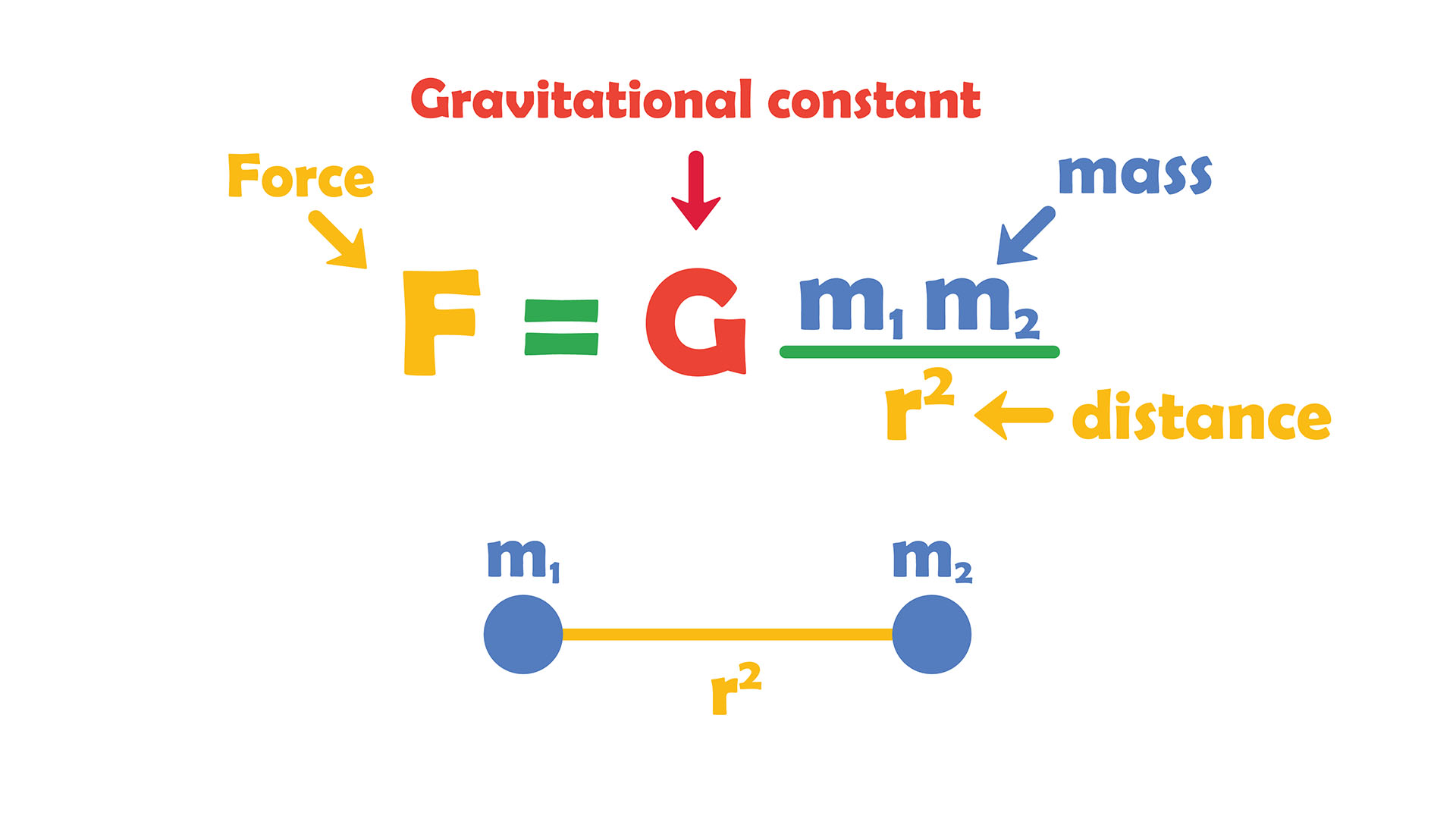
Using this equation, scientists could have theoretically measured Earth's mass by measuring the planet's gravitational force on an object on Earth's surface. But there was a problem: Nobody could figure out a number for G.
Then, in 1797, physicist Henry Cavendish began what became known as the "Cavendish experiments." Using an object called a torsion balance, made up of two rotating rods with lead spheres attached to them, Cavendish found the amount of gravitational force between the two sets by measuring the angle on the rods, which changed as the smaller spheres were attracted to the larger ones.
"His work was very original and made a big impact at the time," John West, a physiologist at the University of California, San Diego, told Live Science.
Knowing the mass and distance between the spheres, Cavendish calculated that G = 6.74×10−11 m3 kg–1 s−2. The International Science Council's Committee on Data currently lists G as 6.67430 x 10-11 m3 kg-1 s-2, only a few decimal points off from Cavendish's original number. Scientists have since used G to calculate Earth's mass using other objects of known mass and arrived at the number of 13.1 septillion pounds we know today.
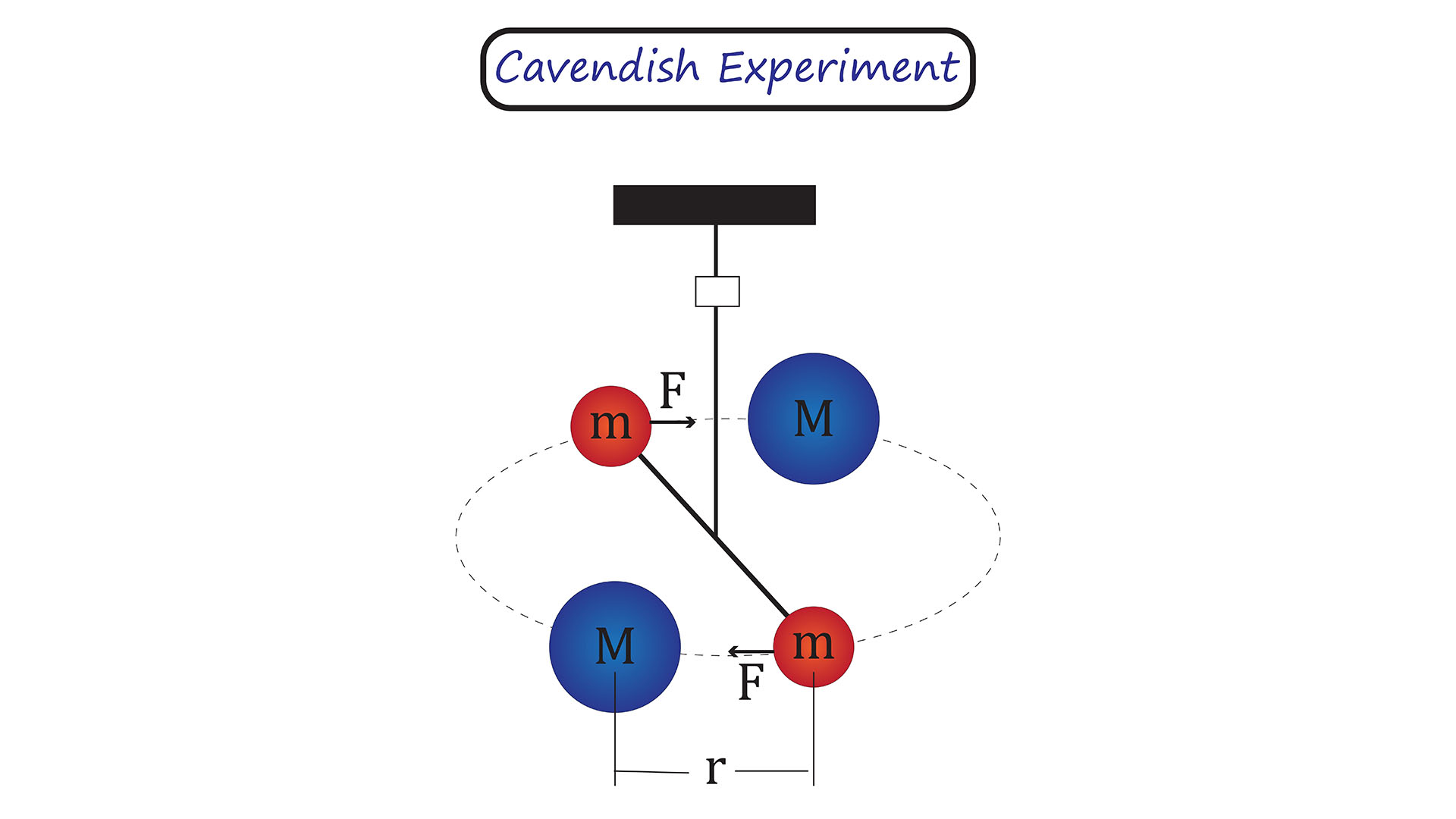
Although it's been more than two centuries since Cavendish's experiment, his torsion balance method is still used today, West said. However, Schlamminger emphasized that although Newton's equation and the torsion balance are important tools, the measurements they deliver remain subject to human error. In the centuries since Cavendish's experiments, different scientists have measured G dozens of times, and each has come up with a slightly different result. The numbers only vary by thousandths of decimal places, but it's enough to change the calculation for Earth's mass and enough to bother the scientists who measure it.
"For us, it's this paper cut in our skin that we have to fix," Schlamminger said.
Despite the frustrations around G, Schlamminger doesn't think the discrepancy in that number is necessarily bad.
"Sometimes it's the cracks that the universe gives us that we can apply our lever to and get more scientific understanding," he said. "This may be a crack the universe is offering us, and we don't want to let that opportunity pass."
Katherine Irving is a freelance science journalist specializing in wildlife and the geosciences. After graduating from Macalester College, where she wrote screenplays, excavated dinosaur bones and vaccinated wolves, Katherine dove straight into internships with Science Magazine and The Scientist. She now contributes to the Science Magazine podcast and loves reporting about the beautiful intricacies of our planet.


