Babylonians used Pythagorean theorem 1,000 years before it was 'invented' in ancient Greece
The tablet is the earliest discovered example of applied geometry.
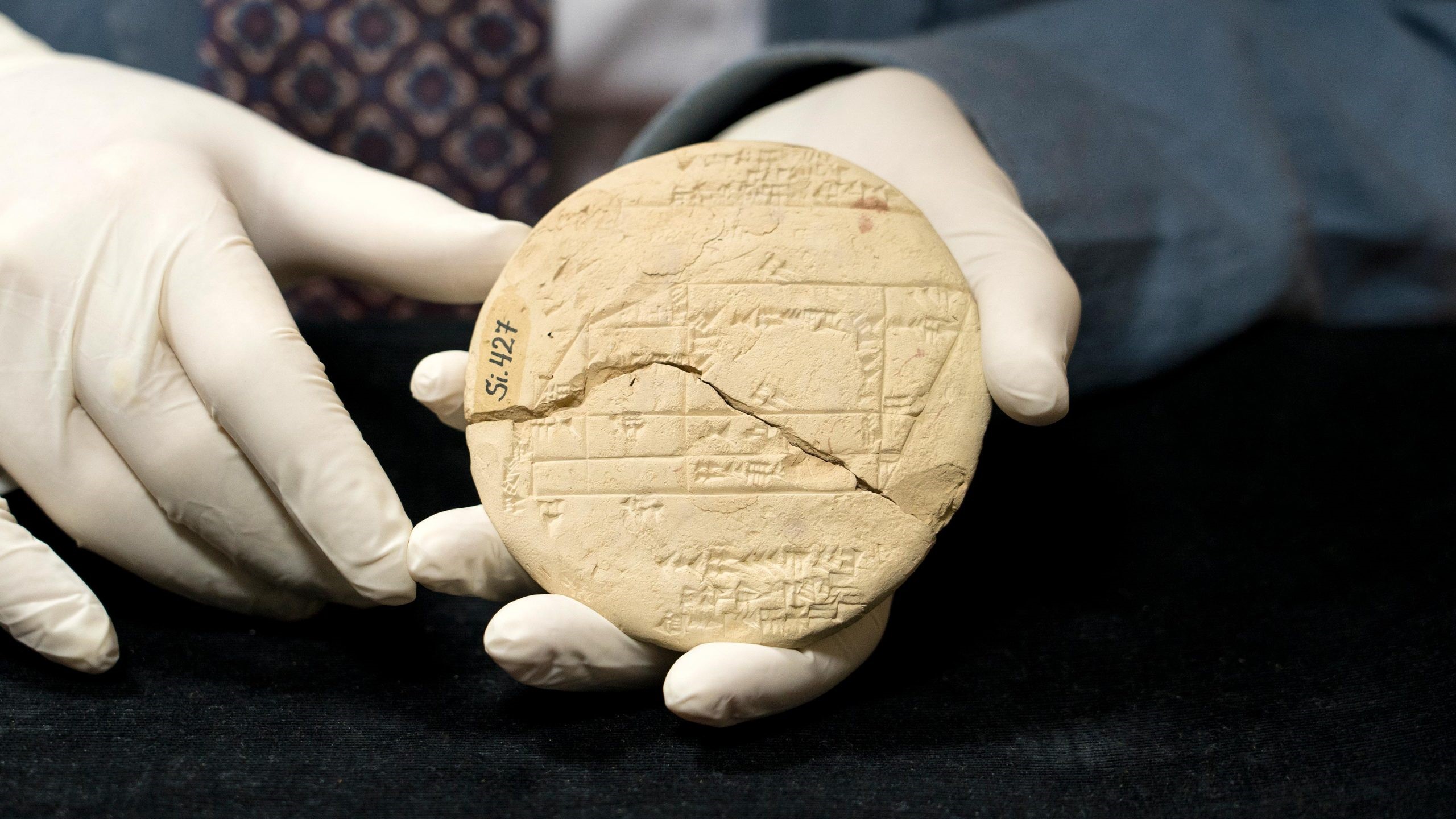
A 3,700-year-old clay tablet has revealed that the ancient Babylonians understood the Pythagorean theorem more than 1,000 years before the birth of the Greek philosopher Pythagoras, who is widely associated with the idea.
The tablet, known as Si.427, was used by ancient land surveyors to draw accurate boundaries and is engraved with cuneiform markings which form a mathematical table instructing the reader on how to make accurate right triangles. The tablet is the earliest known example of applied geometry.
A French archeological expedition first excavated the tablet, which dates to between 1900 and 1600 B.C in what is now Iraq in 1894, and it is currently housed in the Istanbul Archeological Museum.
But it is only just now that researchers have discovered the significance of its ancient markings.
Related: The 11 most beautiful mathematical equations
"It is generally accepted that trigonometry — the branch of maths that is concerned with the study of triangles — was developed by the ancient Greeks studying the night sky," in the second century B.C., Daniel Mansfield, a mathematician at the University of New South Wales in Australia and the discoverer of the tablet's meaning, said in a statement. "But the Babylonians developed their own alternative 'proto-trigonometry' to solve problems related to measuring the ground, not the sky."
According to Mansfield, Si.427 is the Old Babylonian period's only known example of a cadastral document, or a plan surveyors used to define land boundaries. "In this case, it tells us legal and geometric details about a field that's split after some of it was sold off," Mansfield said.
Get the world’s most fascinating discoveries delivered straight to your inbox.
The tablet details a marshy field with various structures, including a tower, built upon it. The tablet is engraved with three sets of Pythagorean triples: three whole numbers for which the sum of the squares of the first two equals the square of the third. The triples engraved on Si.427 are 3, 4, 5; 8, 15, 17; and 5, 12, 13. These were likely used to help determine the land's boundaries.

Though the tablet does not express the Pythagorean theorem in the familiar algebraic form it’s expressed in today, coming up with those triples would have required understanding the general principle that governs the relationship between length of the sides and the hypotenuse.
In 2017, Mansfield had discovered a tablet from the same period, named Plimpton 322, which he identified as containing another trigonometric table. But it wasn't until he saw the triples on Si.427 that he was able to piece together that the ancient Babylonians were using rudimentary trigonometric theory to split up parcels of land.
Si.427 is thought to pre-date Plimpton 322 — and may have even inspired it, Mansfield said.
"There is a whole zoo of right triangles with different shapes. But only a very small handful can be used by Babylonian surveyors. Plimpton 322 is a systematic study of this zoo to discover the useful shapes," Mansfield said, referring to the fact that different types of right triangles can have different interior angles. "This is from a period where land is starting to become private — people started thinking about land in terms of 'my land and your land', wanting to establish a proper boundary to have positive neighbourly relationships. And this is what this tablet immediately says. It's a field being split, and new boundaries are made."
Although the reasons behind the calculations of land boundaries on the tablet aren’t entirely clear, Si.427 does mention a dispute over date-palms on the border between the properties of a prominent individual called Sin-bel-apli and a wealthy female landowner, according to Mansfield. "It is easy to see how accuracy was important in resolving disputes between such powerful individuals," he said.
Even though 1,000 years would pass between the creation of the tablets and the birth of Pythagoras of Samos in 570 B.C. — leading to the formalized Pythagorean rule students are taught in school today — experts have long known that the Greeks inherited mathematical teachings from Egyptians, and the Egyptians in turn from the Babylonians.
What is surprising to Mansfield, however, is the level of theoretical sophistication the tablets reveal the ancient Babylonians to have had at such an early stage of human history.
"Nobody expected that the Babylonians were using Pythagorean triples in this way," he said. "It is more akin to pure mathematics, inspired by the practical problems of the time."
Originally published on Live Science.

Ben Turner is a U.K. based staff writer at Live Science. He covers physics and astronomy, among other topics like tech and climate change. He graduated from University College London with a degree in particle physics before training as a journalist. When he's not writing, Ben enjoys reading literature, playing the guitar and embarrassing himself with chess.