Mathematicians finally identify 'seemingly impossible' number after 32 years, thanks to supercomputers

Mathematicians armed with supercomputers have finally identified the value of a hefty number that was previously thought to be impossible to calculate.

The number, known as the "ninth Dedekind number" or D(9), is actually the 10th in a sequence. Each Dedekind number represents the number of possible configurations of a certain kind of true-false logical operation in different spatial dimensions. (The first number in the sequence is D(0), which represents zero dimensions. This is why D(9), which represents nine dimensions, is the 10th number in the sequence.)

Dedekind numbers get increasingly large for each new dimension, which makes them increasingly difficult to pin down. The eighth Dedekind number, which follows the same rules for eight dimensions, was calculated in 1991. But due to the jump in computing power needed to calculate the ninth, some mathematicians deemed it impossible to calculate its exact value.

But now, two unrelated studies from separate research groups — the first submitted to the preprint server arXiv on April 5 and the second submitted to the same server on April 6 — have done the impossible. The studies —  each using a supercomputer but running different programs —  both produced the exact same number.

Related: Pi calculated to a record-breaking 62.8 trillion digits

The results have not yet been peer-reviewed. But because the studies came to the same conclusion, it is "100% certain" that the number has been properly deciphered, lead author on the second paper, Lennart Van Hirtum, a mathematician at Paderborn University in Germany and lead author on the second paper, told Live Science.

Van Hirtum and his colleagues defended their work during a lecture at Paderborn University on June 27.

What are Dedekind numbers? 

Dedekind numbers were first described by German mathematician Richard Dedekind in the 19th century. The numbers are related to logical problems known as "monotone boolean functions" (MBFs).

Boolean functions are a kind of logic that can take as an input just one of two values — 0 (false) and 1 (true) — and spit out only those two values. In MBFs you can swap a 0 for a 1 in the input, but only if it allows the output to change from a 0 to a 1, not from a 1 to a 0. Dedekind numbers are the output of MBFs where the input is a specific spatial dimension.

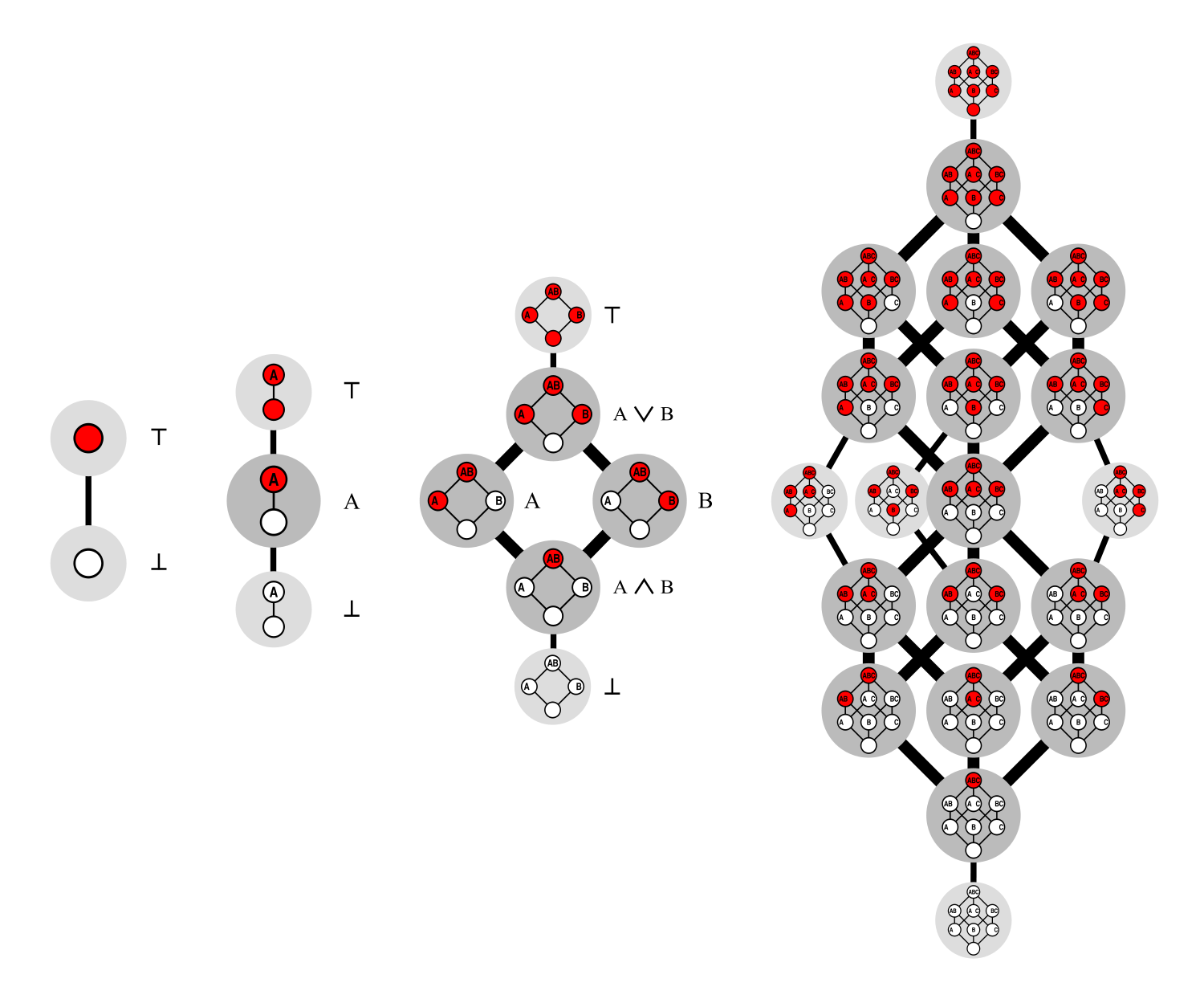
This concept can be pretty confusing for non-mathematicians. But it is possible to visualize what is going on by using shapes to represent the Dedekind numbers for each dimension, Van Hirtum explained. For instance, in the second dimension, the Dedekind number relates to a square, while the third can be represented by a cube, the fourth and higher by hypercubes.

For each dimension, the vertices, or points, of a specific shape represent the possible configurations of MBFs (see picture below). To find the Dedekind number, you can count how many times you can color each vertex from each shape with one of two colors (in this case red and white), but with the stipulation that one color (in this case white) cannot be placed above the other (in this case red).

For zero dimensions, the shape is just a single point and D(0)=2 because the point can be either red or white. For one dimension, the shape is a line with two points and D(1)=3 because both points can either be the same color or red above white. For two dimensions, the shape is a square and D(2)=6 because there are now six possible scenarios where no white dot is above a red dot. And for three dimensions, the shape is a cube, and the number of possible configurations jumps to 20, so D(3)=20.

As the number of dimensions increases, the hypothetical shape becomes an increasingly complex hypercube with an greater number of outcomes, Van Hirtum said. 

The values of the next five Dedekind numbers are 168, 7581, 7828354, 2414682040998 and 56130437228687557907788. 

The newly identified value for D(9) is 286386577668298411128469151667598498812366.

Increasingly complex calculations 

Van Hirtum has been working on identifying D(9) for more than three years. To do this, he created a new type of computer program to enable a supercomputer to process the data in a specific way. If he had used a more basic program, it could have taken up to 100 years to complete the calculations, even with an advanced machine crunching the numbers, he said.

After creating his computer code, Van Hirtum's team spent more than four months using the supercomputer at the University of Leuven in Belgium to process the data. 

However, the calculations did not actually take this long to complete: The nature of the program meant that it was prone to making errors part-way through, which meant the team had to constantly restart the work, Van Hirtum said.

In comparison, the computer used in 1991 to work out D(8) was less powerful than a modern smartphone and completed the task in around 200 hours. A modern laptop could probably have run those calculations in less than 10 minutes, Van Hirtum said.

Van Hirtum believes a similar jump in computer processing power will be required to calculate the 10th Dedekind number. "If we were doing it now, it would require processing power equal to the total power output of the sun," he said, which makes it "practically impossible" to calculate.

The processing power requirements could be reduced using more complex algorithms, Van Hirtum said. 

"But we have sort of hit a wall with how complex the algorithms can get," he added.

However, other mathematicians are still hopeful that D(10) could eventually be calculated, Van Hirtum said.