Mathematicians end decades-long quest to find elusive 'vampire einstein' shape

What has 14 sides, is full of curves, and can perfectly cover a surface with no gaps or overlaps? It's not a riddle — it's a "vampire einstein."

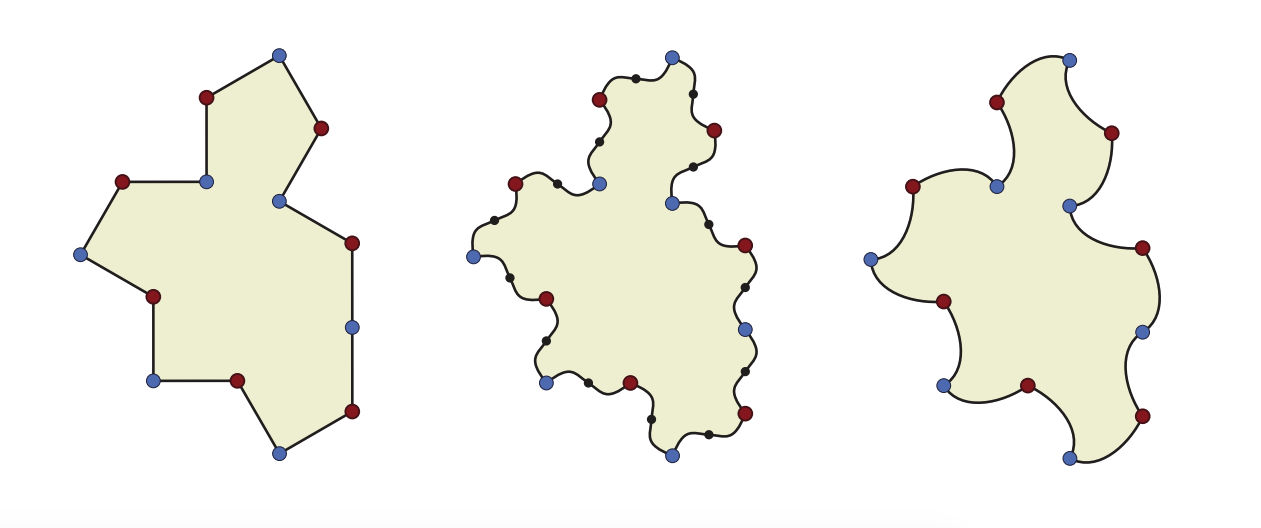
In March, a retired printing technician named David Smith stumbled upon a remarkable discovery in the world of mathematics. He found a 13-sided shape that could completely tile a surface without ever repeating. The shape, nicknamed "the hat" for its vaguely fedora-like shape was the culmination of decades of hunting by mathematicians around the world.

Since 1961 mathematicians had wondered if such a shape could exist. At first, mathematicians found a set of 20,426 shapes that could tile together while creating a pattern that never repeats (in contrast to the tiles on a kitchen floor, which do create a repeating pattern). Eventually, mathematicians found a  set of 104 shapes that could create such a never-repeating tiling. 

Then in the 1970's physicist and Nobel prize winner Roger Penrose found a pair of shapes that together created anon-repeating tiling. And for decades since, mathematicians continued to wonder if the same trick could be done with only a single shape. That semi-mythical shape, known formally as an aperiodic monotile, came to be known as "the einstein," which means "one stone" in German. 

But for all the celebration around Smith's discovery of an einstein tile, there was one small fly in the ointment. In order to create the non-repeating tiling, the "hat" had to work with its mirror image. Technically it's the same shape, just flipped, but some argued that Smith hadn't really found a true einstein.

Now, however, Smith and his colleagues have laid those objections to rest: they've found a shape that can tile a surface without repeating or being flipped. They described the new shape May 28 in a paper published to the preprint database arXiv, though it has not yet been peer reviewed.

The team named their shape the "Spectre," an homage to vampires that can't see their own reflections and thus don't need a mirror. 

"In plane tiling, it is completely standard that tiles may be reflected; nevertheless, some people were dissatisfied that the aperiodic hat monotile requires reflections to tile the plane," co-author Joseph Samuel Meyers wrote on Mastodon. "In our new preprint, we present the Spectre, the first example of a vampire einstein: an aperiodic monotile that tiles the plane without reflections."

To find the ghostly shape, the team started with the original "hat" shape and added an extra side to it. That new shape still required its mirror image to fully tile, but the researchers discovered that by transforming the 14-sided shape's straight edges into curved ones, they could dispense with mirror images and work with just the one shape.