Book Excerpt: 'Now: The Physics of Time' (US 2016)

You are reading the word "now" right now. But what does that mean? What makes the ephemeral moment "now" so special? Its enigmatic character has bedeviled philosophers, priests, and modern-day physicists from Augustine to Einstein and beyond. Einstein showed that the flow of time is affected by both velocity and gravity, yet he despaired at his failure to explain the meaning of "now." Equally puzzling: why does time flow? Some physicists have given up trying to understand, and call the flow of time an illusion, but the eminent experimentalist physicist Richard A. Muller protests. He says physics should explain reality, not deny it. In "Now: The Physics of Time," Muller does more than poke holes in past ideas; he crafts his own revolutionary theory, one that makes testable predictions. He begins by laying out a firm and remarkably clear explanation of the physics building blocks of his theory: relativity, entropy, entanglement, antimatter, and the Big Bang. With the stage then set, he reveals a startling way forward. Below is an excerpt from Muller's "Now: The Physics of Time" (W. W. Norton & Company, 2016).
Physicists are often puzzled by their own equations. It's not always easy to spot the implications, even the most dramatic ones. To help understand their own math, they look at extreme cases to see what happens. And no extreme situation is more extreme in this universe than the extreme of black holes. Looking at black holes gives us important insights into some very peculiar aspects of time.
If you orbit a small black hole (mass of the sun) from a reasonable distance—say, a thousand miles—you'll feel nothing in particular. You are in orbit about a massive object that you can't see. Since you are in orbit, you feel weightless, just as all orbiting astronauts feel. You are not getting sucked in; black holes (despite popular science fiction) do not draw you in. If you were orbiting the sun, at this close distance you'd be inside it and you'd burn to a crisp in a millionth of a second, but the black hole is dark. (Microscopic black holes radiate, but very little comes from big ones.)
The distance around your orbit is 2π times your radial coordinate value of 1,000 miles. If a friend is orbiting the hole, but on the other side, going the opposite direction, then you'll meet after you each go a quarter orbit. But when your friend is diametrically opposite you, the straight-line distance between you is infinite. There is a lot of space near the black hole.
If you fire your retrorockets, stopping your orbital motion, you will indeed be pulled into the hole, just as you would be pulled into any massive object. (The way satellites de-orbit is precisely that: firing retrorockets and then letting gravity pull them in.) Before ten minutes pass in your proper frame, before you are ten minutes older, you will reach the surface of the black hole, at the Schwarzschild radius (discussed in Chapter 3). Now for some astonishing results concerning time. When you hit that surface, ten minutes after beginning your fall, the time measured on the frame of the orbiting station will reach infinity.*[1]
That's right. It takes infinite time to fall into a black hole, measured from the frame of someone outside. From your accelerating frame falling in, it takes only ten minutes. At eleven minutes, the time outside has gone to infinity and beyond.
That's absurd! Possibly, but in classical relativity it is true. Of course, there is no way for you to experience the potential paradox, because beyond infinity is the time on the outside, and once you have entered the black hole you are there forever. There is no measurable contradiction. This is an example of what physicists call censorship. The absurdity is unobservable, so it isn’t really an absurdity.
Get the world’s most fascinating discoveries delivered straight to your inbox.
Are you satisfied with that "beyond infinity but censored" answer? I suspect not. I find it mind-numbing. But everything about time I find mind-numbing. We'll encounter another absurd but censored result with quantum wave functions and entanglement. These examples challenge our sense of reality, and leave an unsatisfied feeling. As Nietzsche said: When you gaze long into an abyss, the abyss also gazes back into you.
Black Holes Don't Suck
Let's return to my statement that black holes don't suck you in, that you orbit a black hole just as you would orbit any other mass. Suppose Mercury were orbiting a black hole that had the same mass as the sun has. How would the orbit be different? According to popular belief, the black hole would suck the tiny planet in. According to general relativity, there would be no difference in the orbit. Of course, Mercury would no longer be hot, since the intense radiation of the sun would be replaced by the cool darkness of the black hole.
Mercury currently orbits the sun at a radial distance of 36 million miles. Suppose you orbited the sun at 1 million miles from its center, just above the solar surface. Aside from the heat, and possibly drag from the solar atmosphere, you would cruise around in a circular orbit and return to your starting point in about ten hours. Now replace the sun with a solar-mass black hole. You would still orbit in ten hours. The gravity, at that distance, would be identical to that of the sun. You have to get very close to a black hole before you notice any special effects. As with any star, the closer you get, the faster you have to move to stay in a circular orbit. As a rule of thumb, you won't see much difference until you are so close that your orbiting speed is approaching the speed of light.
For the sun, the maximum gravity is at the surface, just as it is for the Earth. Go below the surface, and the mass that attracts you, the mass below you, is less than at the surface. At the very center of the sun, the gravity is zero.
For a black hole, however, the surface is close to the center. From the Schwarzschild equation I gave earlier, the radius of a solar black hole can be calculated to be about 2 miles. At a distance of 10 miles, to stay in orbit you would have to move at one-third the speed of light; your orbital period would be one-thousandth of a second. In those conditions, we have to use relativity to do the calculations.
Reaching Lightspeed and Going beyond Infinity
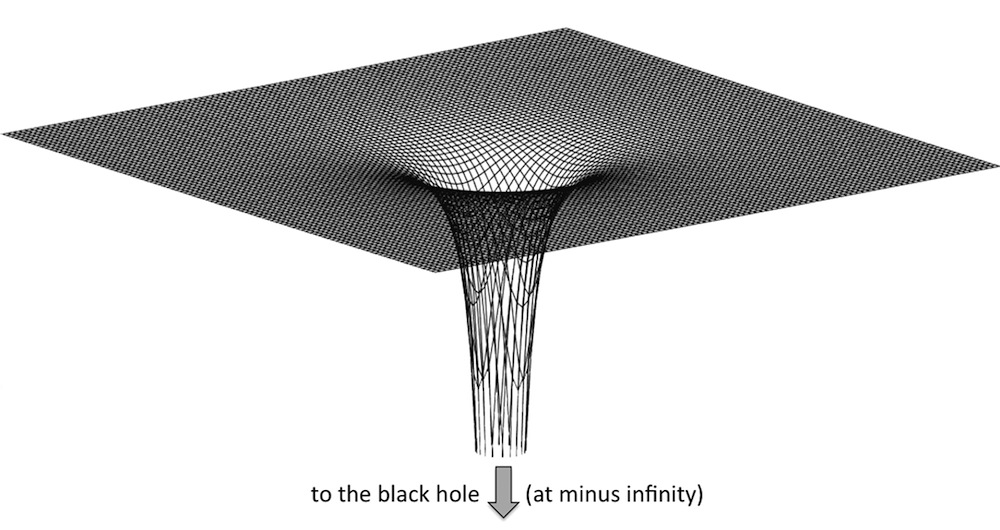
When you get in close to a black hole, time progresses very slowly, and even though the distance around the orbit may be small, there is a lot of space between you and the hole. The space is conventionally depicted to physics students with a diagram such as the one in Figure 7.1. Think of this diagram as representing a black hole in 2D space (the surface). The black hole itself is at the center, below where the curved space is pointing.
This is a useful diagram, but it is somewhat misleading, because it implies that space has to curve into another dimension (for this diagram, that’s the dimension that goes downward) to accommodate the enormous distances close to the black hole. In fact, no such dimension is needed; the space simply gets compressed from relativistic length shortening. The diagram is also used in popular movie depictions of black holes. When Jodie Foster falls into a wormhole in Contact, it looks very much like the diagram in Figure 7.1. (Wormholes look like two almost-black-holes connected before the Schwarzschild radius is reached; fall in one, fly out the other.)
In fact, a black hole would not look at all like the diagram. Unless other things were falling in with you, it would just look like a totally black sphere.
With that caveat, the diagram is useful. It illustrates the basic features of black holes and can be used to answer some simple questions, such as: How far is it from the outside (the relatively flat region) to the surface of the black hole? The answer is infinity. Measure along the falling surface into the hole and you go down forever. You'll hit the radius of the black hole only at the bottom, but that is infinitely far down.
If it is infinity to the surface of the black hole, what did I mean when I said you were 10 miles distant? I confess I was being misleading. I was using the conventional coordinates. The radial coordinate r is defined by saying the distance around the black hole is 2πr, just as in ordinary space. In Figure 7.1, the conventional x, y coordinates are represented by the grid lines. Note how far apart they get in the hole; the large distance between them shows that there is a lot of space in there. Physicists use these conventional coordinates in the equations, but they keep in mind that the distance between the 3-mile marker and the 4-mile marker might indeed be 1,000 miles. Because conventional geometry does not work here, we cannot calculate the distance between two points by just taking the difference in the coordinates.
Actually, There Are No Black Holes
You can find lists of suspected black holes in astrophysics books and online. The Wikipedia article "List of Black Holes" identifies more than seventy. Here's the catch: we have reason to think that none of these are actually black holes.
The way an astronomer identifies a black-hole candidate is to find an object that is very massive, typically several times that of the sun, yet is emitting little or no radiation. Some of the candidate objects emit bursts of X-rays, which are thought to indicate that a chunk of matter (a comet? a planet?) is falling in, and as it does it gets ripped apart and heated by the large differences in gravity across its own body, enough to emit X-rays. Other candidates, called supermassive black holes, contain hundreds of millions of solar masses.
One such supermassive object exists at the center of our own Milky Way Galaxy. We see stars orbiting very close to this center and moving and accelerating very rapidly, indicating the presence of a very large mass. But there is no light, so whatever is pulling these stars is not a star itself. Physics theories suggest that such a large accumulation with no emission can only be a black hole.
Why do I say that there are no true black holes on the list? Recall the calculation showing that it takes infinite time to fall into a black hole. A similar calculation shows that it takes infinite time to form a black hole, measured in our time coordinate. All that material has to fall, effectively, an infinite distance. So unless the black holes already existed at the moment the universe was created, unless they were primordial black holes, they haven’t yet reached true black-hole status; there hasn't been enough time (from our outside proper frame) for the matter to fall the infinite distance that characterizes a true black hole. And there is no reason to think that any of the objects are primordial (although some people speculate that one or more might be).
I am being somewhat pedantic. It takes forever to fall into a black hole, but you get in pretty far in just a few minutes, in your own proper time measured by your own co-falling watch. From the outside frame you’ll never reach the surface, but you’ll be turned into a crepe-like object in relatively short order. So, in some sense, it hardly matters. That may be why, in 1990, Stephen Hawking decided to pay off his 1975 bet with Kip Thorne and concede that Cygnus X-1, the X-ray source in the constellation Cygnus, was indeed a black hole. Technically, Hawking was right, not Thorne. Cygnus X-1 is 99.999 percent of the way to being a black hole, but it will take (from the reference frame of Hawking and Thorne) forever to go the rest of the way.
One particular quantum loophole might circumvent my statement that black holes don't exist. Although it takes forever for a black hole to form in Einstein's original general theory of relativity, it doesn't take too long for one to "almost" form. The time from when the falling matter reaches twice the size of the Schwarzschild radius, to when it reaches within a tiny distance at which quantum effects are big (called a Planck distance, something we'll discuss later), is less than a thousandth of a second. At that point, we don't expect the ordinary general theory of relativity to hold up.
What happens next? The fact is, we don't really know. Many people are working on the theory, but nothing yet has been observed and verified. It is interesting that Hawking paid off his bet with Thorne on whether Cygnus X-1 is truly a black hole; perhaps he felt that it is so close to being a black hole that it hardly matters, or perhaps he became persuaded that the inclusion of quantum physics throws doubt on the infinite-time calculation.
The fact that black holes don't yet really exist—at least "not yet" according to an outside frame—is a fine point, and normally not even mentioned to the nonexpert. But you might be able to win a bet using this "believe it or not" fact.
Another Lightspeed Loophole
In Chapter 5 I gave an example showing how acceleration of your proper frame at 1g could result in the distance between you and a distant object (measured in that accelerating frame) changing at a rate 2.6 times the speed of light. With the Lawrence Berkeley Laboratory electron accelerator BELLA, you could change the distance to Sirius in the electron's proper frame with an equivalent speed of 8.6 billion times lightspeed. You can do even better. You can change distances with infinite speed. Here's how.
Imagine that you and I are a few feet apart, in space, nothing else around. Assume that our proper frames are identical, so in that frame we are both at rest. Now, get a small primordial (completely formed) black hole, maybe one weighing only a few pounds. Plunk it right in between you and me. The gravitational attraction of the black hole is no bigger than for any other object with the same mass, so we don't feel any unusual forces. When the black hole is in place, the straight-line distance between you and me becomes infinite. You can see this on the black-hole diagram. The distance between us has changed. Yet our locations have not.
Have we "moved"? No. Has the distance between you and me changed? Yes. Enormously. Space is fluid and flexible. It can be compressed and stretched. An infinite concentration of space can be moved about easily, since it can be light in mass. That means distances between objects can change at arbitrarily rapid rates, even light-years per second, or faster. It is as if you are moving with super speed—although, in fact, you are not moving at all.
As I mentioned earlier, these concepts will prove important when we discuss modern cosmology in later chapters. In particular, they are the basis for the theory of inflation that is used to explain the puzzling paradox that the universe is remarkably uniform, even though it is so big that it never (apparently) had time to establish such uniformity. More on that later.
Wormholes
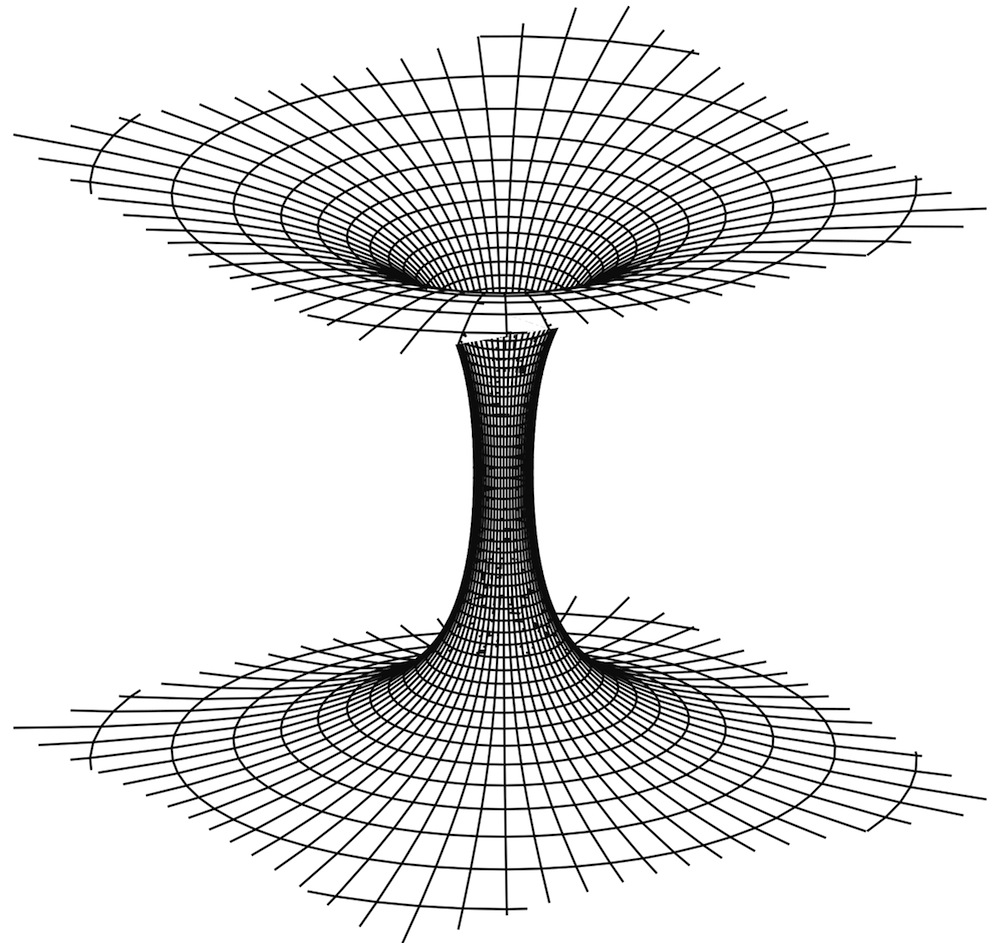
A wormhole is a hypothetical object, similar to a black hole, but instead of the curved space reaching down to an object with huge mass, it eventually spreads out and emerges at a different location. The simplest wormhole is very similar to two not quite black holes connected near the bottom. ("Not quite" means that you can fall in and shoot back out the other side in finite time.) For that to happen, you can imagine that space is folded, so that where the wormhole comes out is across the fold (see Figure 7.2). However, there is no need to imagine that. Remember that the depth to the bottom of the black hole is, from the outside reference frame, infinite in distance. So even though a wormhole isn’t that deep, it could be deep enough to reach anywhere.
A problem with simple wormholes is that calculations show they are not stable. With no mass at the bottom to hold the curved space in place, the wormhole is expected to collapse faster than a person could shoot through it. We might be able to stabilize a wormhole (like stabilizing a coal mine by putting up columns), but current theory says that to do that, we would need something we haven't yet discovered, a kind of particle that has negative energy in its field. Such a field might be possible—at least, we can't rule it out—so science fiction is welcome to go ahead and assume that in the future we will have been able to create stable and useful wormholes.
Wormholes are the current science fiction orthodoxy for rapid travel covering distances of many light-years. Even the Star Trek term warp drive, also used in the Doctor Who series, suggests that the 4D space-time universe is bent into a fifth dimension, bringing distant objects close to each other. The same is true for the movie version of Dune, in which the Guild uses a special material known as spice to bend space. (In the novel, they simply cover distances faster than light, but the movie makes relativistic sense of that ability.)
Wormholes also fascinate science fiction fans because some physicists have argued that they would make travel backward in time possible. As we delve into the meaning of the flow of time, the meaning of now and of time travel, you’ll see why I don't agree that passing through a wormhole could accomplish backward time travel.
It is amazing to me that, although we don't know why time flows, we can talk precisely about the relative flow of time in different locations, and that such flows happen at different rates. Time stretches and shrinks, depending on physics. The next step taken in physics also didn't explain the rate of flow of time, but it did address the simpler question of its direction: Why does time flow forward rather than backward?
[1]* L. Susskind and J. Lindesay discuss this infinite fall time in An Introduction to Black Holes, Information, and the String Theory Revolution (2005), p. 22. They station “Fidos” observers along the fall path who watch the object fall and report to the outsider. “According to this viewpoint, the particle never crosses the horizon but asymptotically approaches it.” Quantum theory could conceivably change this conclusion.
Copyright © 2016 by Richard A. Muller. Used by permission of W. W. Norton & Company, Inc. All rights reserved.