Intro
Nobel Prize winner Ernest Rutherford once said, "all science is either physics or stamp collecting." (Ironically, Rutherford won his Nobel in chemistry, not physics). Physicists may not be the most modest people out there, but if there's one thing they are good at, it's coming up with names for their ideas. Here are some of the best-named physics stuff out there, and what it means.
Ostwald Ripening
Imagine a surface with condensation on it, like a sealed water bottle. At first, the condensation is in the form of lots of tiny water droplets. But if you leave that bottle of water for a while, without disturbing it, you'll notice that all those tiny droplets start to get bigger and bigger. You're observing what physicists call Ostwald Ripening.
The basic premise is that larger droplets are more "energetically favorable" than smaller ones. That's because particles on the surface of a droplet are less stable than those in its middle, and small droplets have a larger proportion of their molecules on the surface than large particles do. To become more stable, the little ones wind up clumping together, forming bigger droplets. So if you leave that water bottle long enough, you can watch those tiny droplets combine and get bigger and bigger.
Even if you've never taken the time to stare at droplets on a water glass, you've experienced Ostwald Ripening if you've ever left ice cream in the fridge too long. That crunchy, icy clump that used to be delicious Rocky Road has experienced Ostwald Ripening. The crystals within the ice cream move from small to large, eventually creating those icky icy clusters.
Von Karman Vortex Street
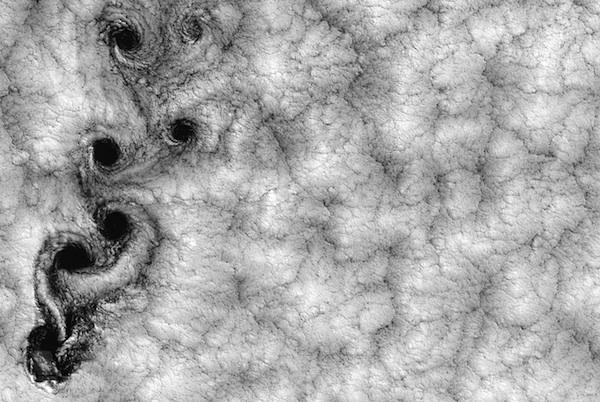
In the field of fluid mechanics, physicists look at the flow of fluids through space and the patterns they make. One of the more beautiful patterns they study are the swirling set of eddies and whirlpools that things like boats leave behind in their wake. As the boat moves through the water, it slices the fluid in half. As the water reunites behind the boat, it creates a pattern of alternating vortices known as the Von Karman vortex street.
The phenomenon is important to all kinds of questions. Tall buildings, chimneys and submarine periscopes, for example, all have to deal with the wind that whips around them. As the wind comes around and then circles back, the force can cause those structures to vibrate forcefully. Some structures, such as antennas and periscopes, have fins to cut the wind and prevent the eddies on either side from meeting.
And it's not just big things that have to deal with the vortex street. As insects beat their wings, they create tiny vortices in the air. But rather than accepting the drag that a vortex can create, the insects turn their wings just a little before their up stroke, so that their wings lift upward along with that swirling current of air.
Tachyonic Antitelephone
Want to send messages into the past? No problem, just pull out your tachyonic antitelephone. The idea for sending messages back in time using physics, at least really started in 1907, when Albert Einstein thought about sending faster than light signals into the past. But Einstein didn't call this a tachyonic antitelephone; it was Gregory Benford who first coined the phrase in 1970. It's one of many such paradoxes, which Benford summarized the like this:
Suppose Alice and Bob enter into the following agreement: Alice will send Bob a message at three o'clock if and only if she does not receive one from him at one o'clock. Upon receiving a message from Alice at two o'clock, Bob immediately sends a message back in time to reach Alice at one o'clock. But the second exchange of messages will take place if, and only if, the first exchange does not take place.
The tachyonic antitelephone requires something called "tachyon particles" which don't even exist in theory, let alone in practice.
The Hairy Ball Theorem
Have you ever tried to comb a coconut? Any physicist would tell you not to. But what they're really talking about is topology.
If you have a ball covered in hairs that are all the same length, there's no way to comb them to all lie nice and flat on the surface of the ball. Think of a tennis ball, of a head of hair. If you try to comb them all nicely, you wind up with a cowlick somewhere and you always wind up with a little bald spot where you start brushing.
This has application to a lot of things, from cyclones to computer graphics. Nanotech engineers used the theorem to create tiny balls of gold hair that would stick to one another. And because wind is like a bunch of hairs sweeping the planet, there will always be one spot on Earth where the air is totally still that bald spot where you started brushing.
The Enormous Theorem
This one refers to a theorem that is, literally, enormous. Also known as the classification of the finite simple groups, the enormous theorem took more than 100 mathematicians, hundreds of journal articles and 15,000 pages to prove, making it the largest mathematical proof ever.
What those mathematicians laid out in that gigantic theorem is that every finite simple group of numbers belongs to one of four categories: cyclic, alternating, simple group of Lie type, or sporadic. Research into these four groups started all the way back in 1832, and wasn't finished until 2004. There are probably only a few mathematicians in the world who understand the proof in full, and it's even unclear what math might gain from its completion. Aside from a world record, that is.
